Из курса физики 8 класса вы знаете, что магнитное поле порождается электрическим током. Оно существует, например, вокруг металлического проводника с током. При этом ток создаётся электронами, направленно движущимися вдоль проводника. Магнитное поле возникает и в том случае, когда ток проходит через раствор электролита, где носителями зарядов являются положительно и отрицательно заряженные ионы, движущиеся навстречу друг другу.
Поскольку электрический ток — это направленное движение заряженных частиц, то можно сказать, что магнитное поле создаётся движущимися заряженными частицами, как положительными, так и отрицательными.
Напомним, что, согласно гипотезе Ампера, в атомах и молекулах вещества в результате движения электронов возникают кольцевые токи.
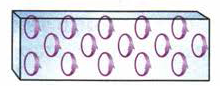
Рис. 85 Иллюстрация гипотезы Ампера
На рис. 85 показано, что в постоянных магнитах эти элементарные кольцевые токи ориентированы одинаково. Поэтому магнитные поля, образующиеся вокруг каждого такого тока, имеют одинаковые направления. Эти поля усиливают друг друга, создавая поле внутри и вокруг магнита.
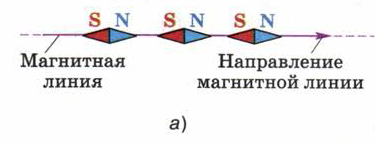
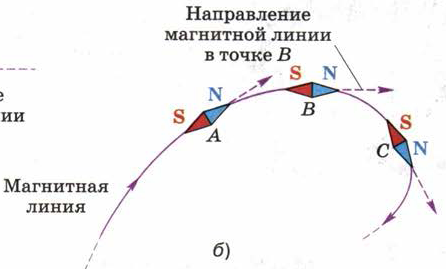
Рис. 86. В любой точке магнитной линии касательная к ней совпадает с осью магнитной стрелки, помещённой в эту точку.
Для наглядного представления магнитного поля используются магнитные линии (их называют также линиями магнитного поля) (В §37 будет дано более точное название и определение этих линий). Напомним, что магнитные линии — это воображаемые линии, вдоль которых расположились бы маленькие магнитные стрелки, помещённые в магнитное поле.
Магнитную линию можно провести через любую точку пространства, в котором существует магнитное поле.
На рис. 86 показано, что магнитная линия (как прямолинейная, так и криволинейная) проводится так, чтобы в любой точке этой линии касательная к ней совпадала с осью магнитной стрелки, помещённой в эту точку.
Магнитные линии являются замкнутыми. Например, картина магнитных линий прямого проводника с током представляет собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику.
Из рисунка 86 видно, что за направление магнитной линии в какой-либо её точке условно принимают направление, которое указывает северный полюс магнитной стрелки, помещённой в эту точку.
В тех областях пространства, где магнитное поле более сильное, магнитные линии изображают ближе друг к другу, т. е. гуще, чем в тех местах, где поле слабее. Например, поле, изображённое на рис. 87, слева сильнее, чем справа.

Рис. 87. Магнитные линии ближе друг к другу в тех местах, где магнитное поле сильнее
Таким образом, по картине магнитных линий можно судить не только о направлении, но и о величине магнитного поля (т. е. о том, в каких точках пространства поле действует на магнитную стрелку с большей силой, а в каких - с меньшей).
Рассмотрим картину линий магнитного поля постоянного полосового магнита (рис. 88). Из курса физики 8 класса вы знаете, что магнитные линии выходят из северного полюса магнита и входят в южный. Внутри магнита они направлены от южного полюса к северному. Магнитные линии не имеют ни начала, ни конца: они либо замкнуты, либо, как средняя линия на рисунке, идут из бесконечности в бесконечность.
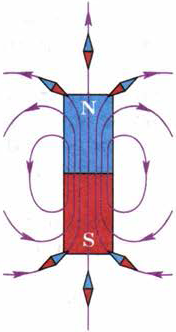
Рис. 88. Картина магнитного поля постоянного полосового магнита
Вне магнита магнитные линии расположены наиболее густо у его полюсов. Значит, возле полюсов поле самое сильное, а по мере удаления от полюсов оно ослабевает. Чем ближе к полюсу магнита расположена магнитная стрелка, тем с большей по модулю силой действует на неё поле магнита. Поскольку магнитные линии искривлены, то направление силы, с которой поле действует на стрелку, тоже меняется от точки к точке.
Таким образом, сила, с которой поле полосового магнита действует на помещённую в это поле магнитную стрелку, в разных точках поля может быть различной как по модулю, так и по направлению.
Такое поле называется неоднородным. Линии неоднородного магнитного поля искривлены, их густота меняется от точки к точке.
Ещё одним примером неоднородного магнитного поля может служить поле вокруг прямолинейного проводника с током. На рис. 89 изображён участок такого проводника, расположенный перпендикулярно плоскости чертежа. Кружочком обозначено сечение проводника. Точка означает, что ток направлен из-за чертежа к нам, как будто мы видим остриё стрелы, указывающей направление тока (ток, направленный от нас за чертёж, обозначают крестиком, как будто мы видим хвостовое оперение стрелы, направленной по току).
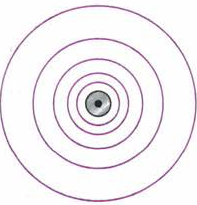
Рис. 89. Магнитные линии магнитного поля, созданного прямолинейным проводником с током
Из этого рисунка видно, что магнитные линии поля, созданного прямолинейным проводником с током, представляют собой концентрические окружности, расстояние между которыми увеличивается по мере удаления от проводника.
В некоторой ограниченной области пространства можно создать однородное магнитное поле, т. е. поле, в любой точке которого сила действия на магнитную стрелку одинакова по модулю и направлению.
На рис. 90 показано магнитное поле, возникающее внутри соленоида — проволочной цилиндрической катушки с током. Поле внутри соленоида можно считать однородным, если длина соленоида значительно больше его диаметра (вне соленоида поле неоднородно, его магнитные линии расположены примерно так же, как у полосового магнита). Из этого рисунка видно, что магнитные линии однородного магнитного поля параллельны друг другу и расположены с одинаковой густотой.
Однородным является также поле внутри постоянного полосового магнита в центральной его части (см. рис. 88).
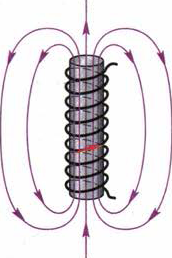
Рис. 90. Магнитное поле соленоида
Для изображения магнитного поля пользуются следующим приёмом. Если линии однородного магнитного поля расположены перпендикулярно к плоскости чертежа и направлены от нас за чертёж, то их изображают крестиками (рис. 91, а), а если из-за чертежа к нам — то точками (рис. 91, б). Как и в случае с током, каждый крестик — это как бы видимое нами хвостовое оперение летящей от нас стрелы, а точка — остриё стрелы, летящей к нам (на обоих рисунках направление стрел совпадает с направлением магнитных линий).


Рис. 91. Линии магнитного поля, направленные перпендикулярно плоскости чертежа:
а — от наблюдателя; б — к наблюдателю.
1. Что является источником магнитного поля?
2. Чем создаётся магнитное поле постоянного магнита?
3. Что такое магнитные линии? Что принимают за их направление в какой-либо её точке?
4. Как располагаются магнитные стрелки в магнитном поле, линии которого прямолинейны; криволинейны?
5.0 чём можно судить по картине линий магнитного поля?
6. Какое магнитное поле — однородное или неоднородное — образуется вокруг полосового магнита; вокруг прямолинейного проводника с током; внутри соленоида, длина которого значительно больше его диаметра?
7. Что можно сказать о модуле и направлении силы, действующей на магнитную стрелку в разных точках неоднородного магнитного поля; однородного магнитного поля?
8. Чем отличается расположение магнитных линий в неоднородном и однородном магнитных полях?
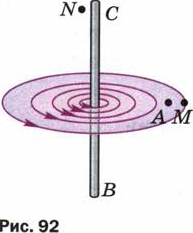
1. На рис. 92 изображён участок ВС проводника с током. Вокруг него в одной из плоскостей показаны линии магнитного поля, созданного этим током. Существует ли магнитное поле в точке А?
2. В какой из точек — А, М или N (см. рис. 92) — магнитное поле тока, протекающего по участку ВС проводника, будет действовать на магнитную стрелку с наибольшей силой; с наименьшей силой?
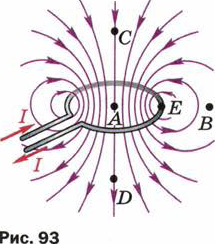
3. На рис. 93 изображён проволочный виток с током и линии магнитного поля, создаваемого этим током.
а) Есть ли среди указанных на рис. точек А, В, С и D такие, в которых поле действовало бы на магнитную стрелку с одинаковой по модулю силой? (АС = AD, АЕ = ВЕ.) Если такие точки есть, укажите их.
б) В какой из точек — А, В, С или D — поле действует на магнитную стрелку с наибольшей силой?
в) Можно ли найти такие точки, в которых сила действия поля на магнитную стрелку была бы одинакова как по модулю, так и по направлению? Если да, то сделайте в тетради рисунок и укажите на нём хотя бы две пары таких точек.
На рис. 94 показано расположение магнитных стрелок вокруг проводника с током, расположенного перпендикулярно плоскости чертежа. Из рисунка видно, что изменение направления тока приводит к повороту всех магнитных стрелок на 180°. Причём в обоих случаях оси стрелок располагаются по касательным к магнитным линиям.
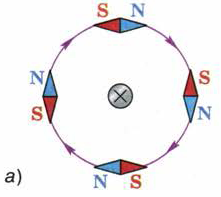
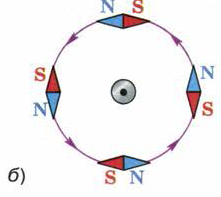
Рис. 94. Направление линий магнитного поля, созданного проводником с током,
зависит от направления тока в проводнике
Следовательно, направление линий магнитного поля тока зависит от направления тока в проводнике.
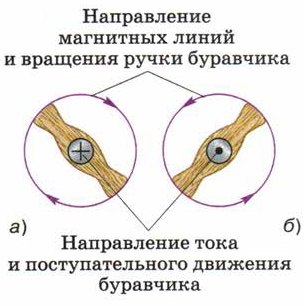
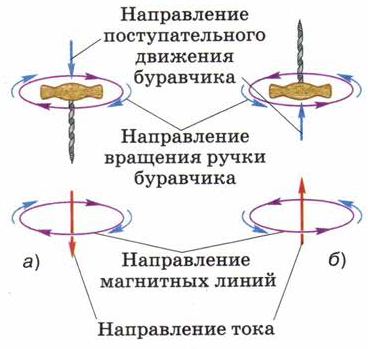
Эта связь может быть выражена правилом буравчика (или правилом правого винта), которое заключается в следующем: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока (рис. 95, 96).
 |
 |
|
Рис. 95. Применение правила буравчика: проводник с током расположен перпендикулярно плоскости чертежа. |
Рис. 96. Применение правила буравчика: проводник с током расположен в плоскости чертежа. |

Рис. 97. Определение направления линий магнитного поля внутри соленоида
С помощью правила буравчика по направлению тока можно определить направление линий магнитного поля, создаваемого этим током, а по направлению линий магнитного поля — направление тока, создающего это поле.
Для определения направления линий магнитного поля соленоида удобнее пользоваться другим правилом, которое иногда называют правилом правой руки. Это правило формулируется так: если обхватить соленоид ладонью правой руки, направив четыре пальца по направлению тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида (рис. 97).
Вы уже знаете, что магнитное поле соленоида (см. рис. 90) подобно полю постоянного полосового магнита (см. рис. 88). Соленоид, как и магнит, имеет полюсы: тот конец соленоида, из которого магнитные линии выходят, является северным полюсом, а тот, в который входят, — южным.
Зная направление тока в соленоиде, по правилу правой руки можно определить направление магнитных линий поля внутри него, а значит, и его магнитные полюсы.
И наоборот, по направлению магнитных линий поля внутри соленоида или расположению его полюсов можно определить направление тока в витках соленоида.
Правило правой руки можно применять и для определения направления линий магнитного поля в центре витка с током.
1. Опишите опыт, подтверждающий связь между направлением тока в проводнике и направлением линий магнитного поля, созданного проводником. 2. Сформулируйте правило буравчика. 3. Что можно определить, используя правило буравчика? 4. Сформулируйте правило правой руки. 5. Что можно определить с помощью правила правой руки?

1. На рис. 98 изображён проволочный прямоугольник, направление тока в нём показано стрелками. Перечертите рисунок в тетрадь и, пользуясь правилом буравчика, начертите вокруг каждой из его четырёх сторон по одной магнитной линии, указав стрелкой её направление.
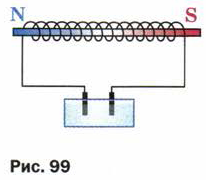
2. Определите направление тока в катушке и полюсы источника тока (рис. 99), если при прохождении тока в катушке возникают указанные на рис. магнитные полюсы.
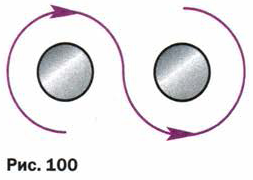
3. Направление тока в витках обмотки подковообразного электромагнита показано стрелками (рис. 100). Определите полюсы электромагнита.
4*. Параллельные провода, по которым текут токи одного направления, притягиваются, а параллельные пучки электронов, движущихся в одном направлении, отталкиваются. В каком из этих случаев взаимодействие обусловлено электрическими силами, а в каком — магнитными? Почему вы так считаете?
Из курса физики 8 класса вы знаете, что на всякий проводник с током, помещённый в магнитное поле и не совпадающий с его магнитными линиями, это поле действует с некоторой силой.
Наличие такой силы можно показать с помощью установки, изображённой на рис. 101. Трёхсторонняя рамка ABCD, изготовленная из медной проволоки, подвешена на крюках так, что может свободно отклоняться от вертикали. Сторона ВС находится в области наиболее сильного магнитного поля дугообразного магнита, располагаясь между его полюсами (рис. 101, а). Рамка присоединена к источнику тока последовательно с реостатом и ключом.
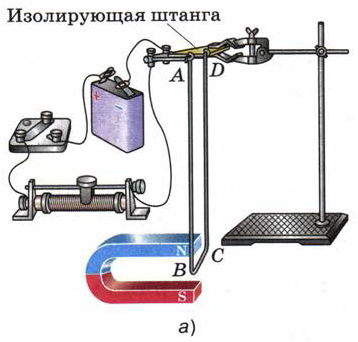
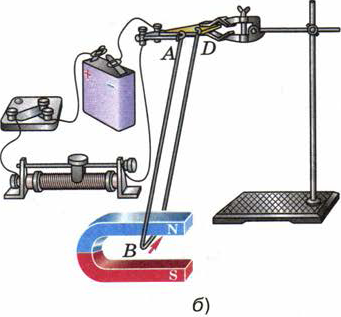
Рис. 101. Действие магнитного поля на проводник с током.
При замыкании ключа в цепи возникает электрический ток, и сторона ВС втягивается в пространство между полюсами (рис. 101, б).
Если убрать магнит, то при замыкании цепи проводник ВС двигаться не будет. Значит, со стороны магнитного поля на проводник с током действует некоторая сила, отклоняющая его от первоначального положения.
Действие магнитного поля на проводник с током может быть использовано для обнаружения магнитного поля в данной области пространства.
Конечно, обнаружить магнитное поле проще с помощью компаса. Но действие магнитного поля на находящуюся в нём магнитную стрелку компаса, по существу, тоже сводится к действию поля на элементарные электрические токи, циркулирующие в молекулах и атомах магнитного вещества, из которого изготовлена стрелка.
Таким образом, магнитное поле создаётся электрическим током и обнаруживается по его действию на электрический ток.
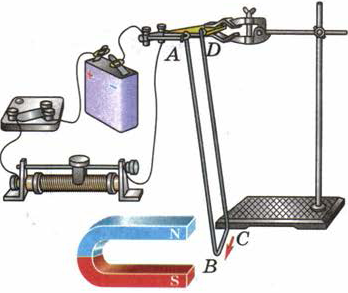
Рис. 102. Направление силы, действующей в магнитном поле на проводник с током,
зависит от направления тока
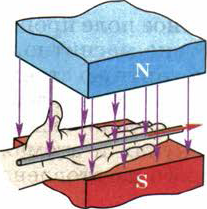
Рис. 103. Применение правила левой руки к проводнику с током
Изменим направление тока в цепи, поменяв местами провода в гнёздах изолирующей штанги (рис. 102). При этом изменится и направление движения проводника ВС, а значит, и направление действующей на него силы.
Направление силы изменится и в том случае, если, не меняя направления тока, поменять местами полюсы магнита (т. е. изменить направление линий магнитного поля).
Следовательно, направление тока в проводнике, направление линий магнитного поля и направление силы, действующей на проводник, связаны между собой.
Направление силы, действующей на проводник с током в магнитном поле, можно определить, пользуясь правилом левой руки.
В наиболее простом случае, когда проводник расположен в плоскости, перпендикулярной линиям магнитного поля, это правило заключается в следующем: если левую руку расположить так, чтобы линии магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца были направлены по току, то отставленный на 90° большой палец покажет направление действующей на проводник силы (рис. 103).
Пользуясь правилом левой руки, следует помнить, что за направление тока в электрической цепи принимается направление от положительного полюса источника тока к отрицательному. Другими словами, четыре пальца левой руки должны быть направлены против движения электронов в электрической цепи. В таких проводящих средах, как растворы электролитов, где электрический ток создаётся движением зарядов обоих знаков, направление тока, а значит, и направление четырёх пальцев левой руки совпадает с направлением движения положительно заряженных частиц.
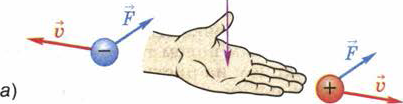
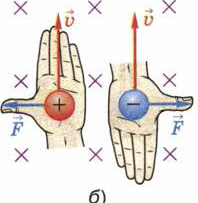
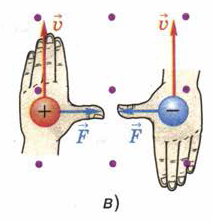
Рис. 104. Применение правила левой руки к заряженным частицам,
движущимся в магнитном поле
С помощью правила левой руки можно определить направление силы, с которой магнитное поле действует на отдельно взятые движущиеся в нём частицы, как положительно, так и отрицательно заряженные.
Для наиболее простого случая, когда частица движется в плоскости, перпендикулярной магнитным линиям, это правило формулируется следующим образом: если левую руку расположить так, чтобы линии магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца были направлены по движению положительно заряженной частицы (или против движения отрицательно заряженной), то отставленный на 90° большой палец покажет направление действующей на частицу силы (рис. 104).
По правилу левой руки можно также определить направление тока (если знаем, как направлены линии магнитного поля и действующая на проводник сила), направление магнитных линий (если известны направления тока и силы), знак заряда движущейся частицы (по направлению магнитных линий, силы и скорости движения частицы) и т. д.
Следует отметить, что сила действия магнитного поля на проводник с током или движущуюся заряженную частицу равна нулю, если направление тока в проводнике или скорость частицы совпадают с линией магнитной индукции или параллельны ей (рис. 105).
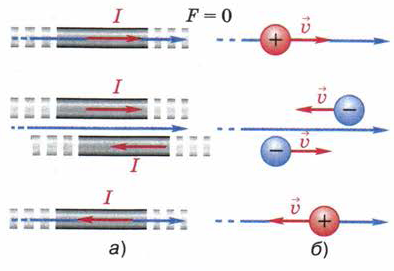
Рис. 105. Магнитное поле не действует в случаях, если прямолинейный проводник с током
или скорость движущейся заряженной частицы параллельны линиям магнитного поля или совпадают с ними
1. Какой опыт позволяет обнаружить наличие силы, действующей на проводник с током в магнитном поле?
2. Как обнаруживается магнитное поле?
3. От чего зависит направление силы, действующей на проводник с током в магнитном поле?
4. Сформулируйте правило левой руки для находящегося в магнитном поле проводника с током; для движущейся в этом поле заряженной частицы.
5. Что можно определить, пользуясь правилом левой руки?
6. В каком случае сила действия магнитного поля на проводник с током или движущуюся заряженную частицу равна нулю?
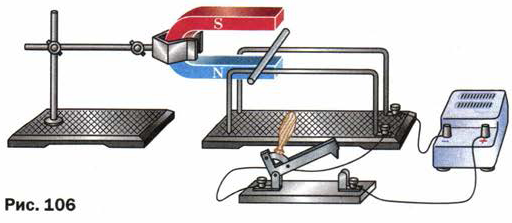
1. В какую сторону покатится лёгкая алюминиевая трубочка при замыкании цепи (рис. 106)?
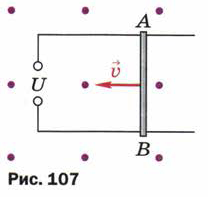
2. На рис. 107 изображены два оголённых проводника, соединённых с источником тока, и лёгкая алюминиевая трубочка АВ. Вся установка находится в магнитном поле. Определите направление тока в трубочке АВ, если в результате взаимодействия этого тока с магнитным полем трубочка катится по проводникам в направлении, указанном на рисунке. Какой полюс источника тока является положительным, а какой — отрицательным?

3. Между полюсами магнитов (рис. 108) расположены четыре проводника с током. Определите, в какую сторону движется каждый из них.
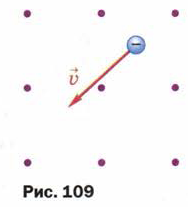
4. Отрицательно заряженная частица движется со скоростью V в магнитном поле (рис. 109). Укажите направление силы, с которой поле действует на частицу.
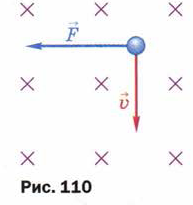
5. Магнитное поле действует с силой F на частицу, движущуюся со скоростью V (рис. 110). Определите знак заряда частицы.
Многие из вас наверняка замечали, что одни магниты создают в пространстве более сильные поля, чем другие. Например, поле первого магнита, изображённого на рис. 111, сильнее, чем второго. Действительно, при одном и том же расстоянии до гвоздей, рассыпанных на столе, сила притяжения к первому магниту оказалась достаточной для преодоления силы тяжести гвоздей, а сила притяжения ко второму — нет.

Рис. 111. Магнитное поле первого магнита сильнее, чем второго
Какой же величиной можно охарактеризовать магнитное поле?
Магнитное поле характеризуется векторной физической величиной, которая обозначается символом В и называется индукцией магнитного поля (или магнитной индукцией).
Поясним, что это за величина.
Напомним, что магнитное поле может действовать с определённой силой на помещённый в него проводник с током.
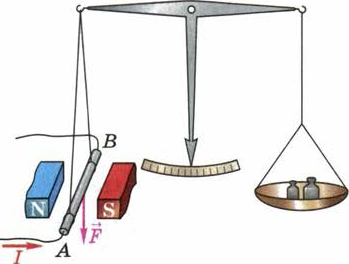
Рис. 112. Опыт по измерению силы, действующей на помещённый в магнитное поле проводник с током
Поместим прямолинейный участок проводника АВ с током в магнитное поле перпендикулярно его магнитным линиям (рис. 112). При показанном на рис. направлении силы тока I в проводнике и расположении полюсов магнита действующая на проводник сила F, согласно правилу левой руки, будет направлена вниз. Определить эту силу можно, вычислив вес гирьки, которую приходится добавлять на правую чашу весов для уравновешивания силы F.
Опыты показывают, что модуль этой силы зависит от самого магнитного поля — более мощный магнит действует на данный проводник с большей силой. Кроме того, сила действия магнитного поля на проводник пропорциональна длине l этого проводника и силе тока I в нём.
Отношение же модуля силы F к длине проводника l и силе тока I т. е. — есть величина постоянная. Она не зависит ни от длины проводника, ни от силы тока в нём. Отношение — зависит только от поля и может служить его количественной характеристикой.
Эта величина и принимается за модуль вектора магнитной индукции:
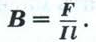
Модуль вектора магнитной индукции В равен отношению модуля силы F, с которой магнитное поле действует на расположенный перпендикулярно магнитным линиям проводник с током, к силе тока I в проводнике и его длине l.
По этой формуле можно определить индукцию однородного магнитного поля.
В СИ единица магнитной индукции называется тесла (Тл) в честь югославского электротехника Николы Тесла.
Установим взаимосвязь между единицей магнитной индукции и единицами других величин СИ:
1 Тл = 1 H/(A•M) .
До сих пор для графического изображения магнитных полей мы пользовались линиями, которые условно называли магнитными линиями или линиями магнитного поля. Более точное название магнитных линий — линии магнитной индукции (или линии индукции магнитного поля).
Линиями магнитной индукции называются линии, касательные к которым в каждой точке поля совпадают с направлением вектора магнитной индукции.
Данное определение линий магнитной индукции можно пояснить с помощью рисунка 113. На нём изображён проводник с током, расположенный перпендикулярно плоскости чертежа. Окружность вокруг проводника представляет собой одну из линий индукции магнитного поля, созданного протекающим по проводнику током. Проведённые к этой окружности касательные в любой точке совпадают с вектором магнитной индукции.
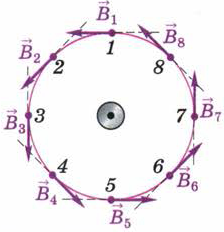
Рис. 113. Вектор магнитной индукции прямого проводника с током
направлен по касательной в каждой точке поля
Теперь, пользуясь термином «магнитная индукция», назовём основные признаки однородного и неоднородного магнитных полей.
В однородном магнитном поле (рис. 114) вектор магнитной индукции В во всех произвольно выбранных точках поля одинаков как по модулю, так и по направлению.
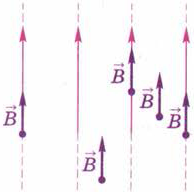
Рис. 114. Во всех точках однородного магнитного поля вектор магнитной
индукции B
одинаков по модулю и направлению
Сравним это поле с двумя неоднородными полями: полем постоянного полосового магнита (рис. 115, а) и полем тока, протекающего по прямолинейному участку проводника (рис. 115, б).
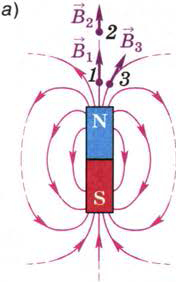
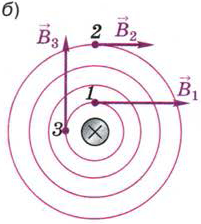
Рис. 115. В разных точках неоднородного магнитного поля вектор магнитной индукции
может быть различным как по модулю, так и по направлению
Легко заметить, что в неоднородных полях, в отличие от однородного, вектор магнитной индукции меняется от точки к точке. Например, в каждом из рассматриваемых неоднородных полей при переходе из точки 1 в точку 2 вектор магнитной индукции меняется по модулю, при переходе из точки 1 в точку 3 — по направлению, при переходе из точки 2 в точку 3 вектор магнитной индукции меняется как по модулю, так и по направлению.
Магнитное поле называется однородным, если во всех его точках магнитная индукция В одинакова. В противном случае поле называется неоднородным.
Чем больше магнитная индукция в данной точке поля, тем с большей силой будет действовать поле в этой точке на магнитную стрелку или движущийся электрический заряд.
1. Как называется векторная величина, которая служит количественной характеристикой магнитного поля?
2. По какой формуле определяется модуль вектора магнитной индукции однородного магнитного поля?
3. Что называется линиями магнитной индукции?
4. В каком случае магнитное поле называется однородным, а в каком — неоднородным?
5. Как зависит сила, действующая в данной точке магнитного поля на магнитную стрелку или движущийся заряд, от магнитной индукции в этой точке?
1. В однородное магнитное поле перпендикулярно линиям магнитной индукции поместили прямолинейный проводник, по которому протекает ток. Сила тока в проводнике 4 А. Определите индукцию этого поля, если оно действует с силой 0,2 Н на каждые 10 см длины проводника.
2. Проводник с током поместили в однородное магнитное поле перпендикулярно линиям магнитной индукции В. Через некоторое время силу тока в проводнике уменьшили в 2 раза. Изменилась ли при этом индукция В магнитного поля, в которое был помещён проводник? Сопровождалось ли уменьшение силы тока изменением какой-либо другой физической величины? Если да, то что это за величина и как она изменилась?
На рис. 116, а изображён проволочный контур, помещённый в однородное магнитное поле. Принято говорить, что контур в магнитном поле пронизывается определённым магнитным потоком Ф, или потоком вектора магнитной индукции.
Опыты показывают, что магнитный поток сквозь контур пропорционален модулю вектора индукции однородного магнитного поля и площади, ограниченной этим контуром. Кроме того, магнитный поток зависит от того, как расположена плоскость контура по отношению к линиям магнитной индукции.
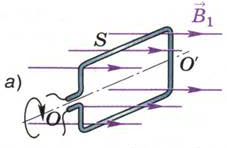
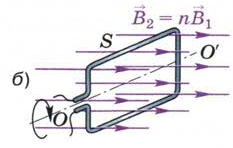
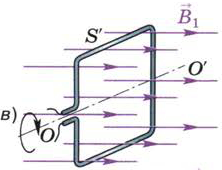
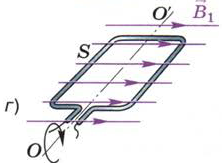
Рис. 116. Зависимость магнитного потока, пронизывающего площадь контура,
от модуля вектора магнитной индукции, площади контура и от ориентации плоскости контура
по отношению к линиям магнитной индукции
Допустим, что индукция магнитного поля, пронизывающего ограниченную контуром площадь, стала больше. Это могло произойти, например, в результате увеличения силы тока, создающего это магнитное поле, или при перемещении контура в другое, более сильное поле.
Поскольку магнитный поток пропорционален индукции магнитного поля, то при её увеличении в n раз (от значения В1 до значения В2 = nВ1, как показано на рис. 116, а, б) во столько же раз возрастёт и поток Ф, пронизывающий площадь S данного контура.
При том же самом магнитном поле с индукцией В1 магнитный поток, пронизывающий большую площадь S' (рис. 116, в), будет во столько же раз больше потока через площадь S (см. рис. 116, а), во сколько раз S' больше, чем S.
Если плоскость контура перпендикулярна линиям магнитной индукции (см. рис. 116, а), то при данной индукции В1 поток Ф, пронизывающий ограниченную этим контуром площадь S, максимален.
При вращении контура вокруг оси ОО' проходящий сквозь него магнитный поток уменьшается (по закону косинуса) и становится равным нулю, когда плоскость контура располагается параллельно линиям магнитной индукции (рис. 116, г). В этом случае линии магнитной индукции как бы скользят по плоскости рамки, не пронизывая её.
Таким образом,
магнитный поток, пронизывающий площадь контура, меняется при изменении модуля вектора магнитной индукции B, площади контура S и при вращении контура, т. е. при изменении его ориентации по отношению к линиям индукции магнитного поля.
Если же контур вращается так, что при любом его положении линии магнитной индукции лежат в плоскости контура, не пересекая ограниченную им площадь (рис. 117), то поток не меняется: в любой момент времени он равен нулю.
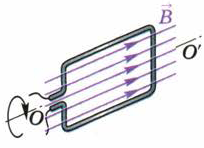
Рис. 117. Магнитный поток равен нулю, если линии магнитной индукции лежат в плоскости контура
1. От чего зависит магнитный поток, пронизывающий площадь плоского контура, помещённого в однородное магнитное поле?
2. Как меняется магнитный поток при увеличении в п раз магнитной индукции, если ни площадь, ни ориентация контура не меняются?
3. При какой ориентации контура по отношению к линиям магнитной индукции магнитный поток, пронизывающий площадь этого контура, максимален; равен нулю?
4. Меняется ли магнитный поток при таком вращении контура, когда линии магнитной индукции то пронизывают его, то скользят по его плоскости?
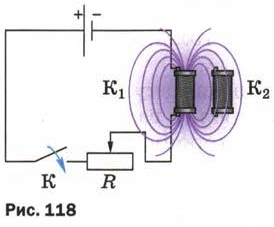
Проволочная катушка K1 со стальным сердечником включена в цепь источника постоянного тока последовательно с реостатом R и ключом К (рис. 118). Электрический ток, протекающий по виткам катушки K1 , создаёт в пространстве вокруг неё магнитное поле. В поле катушки K1 находится такая же катушка К2. Каким образом можно менять магнитный поток, пронизывающий катушку К2? Рассмотрите все возможные варианты.
Вы уже знаете, что вокруг электрического тока всегда существует магнитное поле. Электрический ток и магнитное поле неотделимы друг от друга.
Но если электрический ток, как говорят, «создаёт» магнитное поле, то не существует ли обратного явления? Нельзя ли с помощью магнитного поля «создать» электрический ток?
Такую задачу в начале XIX в. пытались решить многие учёные. Поставил её перед собой и английский учёный Майкл Фарадей. «Превратить магнетизм в электричество» — так записал в своём дневнике эту задачу Фарадей в 1822 г. Почти 10 лет упорной работы потребовалось учёному для её решения.

МАЙКЛ ФАРАДЕЙ
(1791 — 1867)
Английский физик. Открыл явление электромагнитной индукции, экстратоки при замыкании и размыкании
Чтобы понять, как Фарадею удалось «превратить магнетизм в электричество», выполним некоторые опыты Фарадея, используя современные приборы.
На рис. 119, а показано, что если в катушку, замкнутую на гальванометр, вдвигается магнит, то стрелка гальванометра при этом отклоняется, указывая на появление индукционного (наведённого) тока в цепи катушки. Индукционный ток в проводнике представляет собой такое же упорядоченное движение электронов, как и ток, полученный от гальванического элемента или аккумулятора. Название "индукционный» указывает только на причину его возникновения.
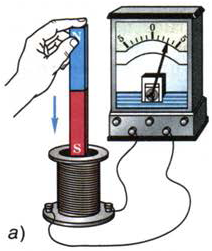
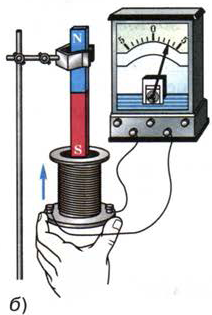
Рис. 119. Возникновение индукционного тока при движении магнита и катушки относительно друг друга
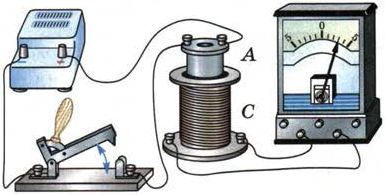
Рис. 120. Возникновение индукционного тока при замыкании и размыкании электрической цепи
При извлечении магнита из катушки снова наблюдается отклонение стрелки гальванометра, но в противоположную сторону, что указывает на возникновение в катушке тока противоположного направления.
Как только движение магнита относительно катушки прекращается, прекращается и ток. Следовательно, ток в цепи катушки существует только во время движения магнита относительно катушки.
Опыт можно изменить. На неподвижный магнит будем надевать катушку и снимать её (рис. 119, б). И опять можно обнаружить, что во время движения катушки относительно магнита в цепи снова появляется ток.
На рис. 120 изображена катушка А, включённая в цепь источника тока. Эта катушка вставлена в другую катушку С, подключённую к гальванометру. При замыкании и размыкании цепи катушки А в катушке С возникает индукционный ток.
Можно вызвать появление индукционного тока в катушке С и путём изменения силы тока в катушке А или движением этих катушек относительно друг друга.
Проделаем ещё один опыт. Поместим в магнитное поле плоский контур из проводника, концы которого соединим с гальванометром (рис. 121, а). При повороте контура гальванометр отмечает появление в нём индукционного тока. Ток будет появляться и в том случае, если рядом с контуром или внутри него вращать магнит (рис. 121, б).
Во всех рассмотренных опытах индукционный ток возникал при изменении магнитного потока, пронизывающего охваченную проводником площадь.
В случаях, изображённых на рисунках 119 и 120, магнитный поток менялся за счёт изменения индукции магнитного поля. Действительно, при движении магнита и катушки относительно друг друга (см. рис. 119) катушка попадала в области поля с большей или меньшей магнитной индукцией (так как поле магнита неоднородное). При замыкании и размыкании цепи катушки А (см. рис. 120) индукция создаваемого этой катушкой магнитного поля менялась за счёт изменения силы тока в ней.
При вращении проволочного контура в магнитном поле (см. рис. 121, а) или магнита относительно контура (см. рис. 121, б) магнитный поток менялся за счёт изменения ориентации этого контура по отношению к линиям магнитной индукции.
Таким образом,
при всяком изменении магнитного потока, пронизывающего площадь, ограниченную замкнутым проводником, в этом проводнике возникает электрический ток, существующий в течение всего процесса изменения магнитного потока.
В этом и заключается явление электромагнитной индукции.
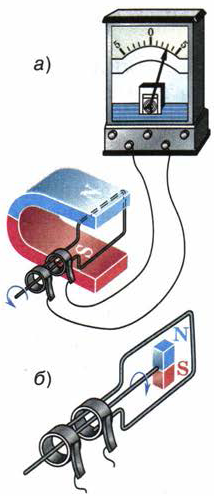
Рис. 121. При вращении контура в магнитном поле(магнита относительно контура)
изменение магнитного потока приводит к возникновению индукционного тока
Открытие электромагнитной индукции принадлежит к числу самых замечательных научных достижений первой половины XIX в. Оно вызвало появление и бурное развитие электротехники и радиотехники.
На основании явления электромагнитной индукции были созданы мощные генераторы электрической энергии, в разработке которых принимали участие учёные и техники разных стран.
Среди них были и наши соотечественники:
Михаил Иосифович Доливо-Добровольский
и другие, внёсшие большой вклад в развитие электротехники.
1. С какой целью ставились опыты, изображённые на рисунках 119-121? Как они проводились?
2. При каком условии в опытах (см. рис. 119, 120) в катушке, замкнутой на гальванометр, возникал индукционный ток?
3. В чём заключается явление электромагнитной индукции?
4. В чём важность открытия явления электромагнитной индукции?
1. Как создать кратковременный индукционный ток в катушке К2, изображённой на рис. 118?
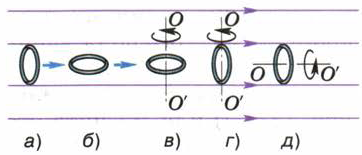
Рис. 122
2. Проволочное кольцо помещено в однородное магнитное поле (рис. 122). Стрелочки, изображённые рядом с кольцом, показывают, что в случаях а и б кольцо движется прямолинейно вдоль линий индукции магнитного поля, а в случаях в, гид — вращается вокруг оси ОО’. В каких из этих случаев в кольце может возникнуть индукционный ток?
В предыдущем параграфе были рассмотрены опыты по получению индукционного тока и установлена причина его возникновения.
Как же направлен индукционный ток? Для ответа на этот вопрос воспользуемся прибором, изображённым на рис. 123. Он представляет собой узкую алюминиевую пластинку с алюминиевыми кольцами на концах. Одно кольцо сплошное, другое имеет разрез. Пластинка с кольцами помещена на стойку и может свободно вращаться вокруг вертикальной оси.
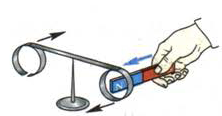
Рис. 123. При приближении к сплошному кольцу любого полюса магнита кольцо отталкивается от него
Возьмём полосовой магнит и внесём его в кольцо с разрезом — кольцо останется на месте. Если же вносить магнит в сплошное кольцо, то оно будет отталкиваться, уходить от магнита, поворачивая при этом всю пластинку. Результат будет точно таким же, если магнит будет повёрнут к кольцам не северным полюсом (как показано на рисунке), а южным. Объясним наблюдаемые явления.
При приближении к кольцу любого полюса магнита, поле которого является неоднородным, проходящий сквозь кольцо магнитный поток увеличивается (рис. 124). При этом в сплошном кольце возникает индукционный ток, а в кольце с разрезом тока не будет.

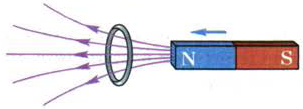
Рис. 124. Возникновение индукционного тока в сплошном кольце при приближении к кольцу магнита
Ток в сплошном кольце создаёт в пространстве магнитное поле, благодаря чему кольцо приобретает свойства магнита. Взаимодействуя с приближающимся полосовым магнитом, кольцо отталкивается от него. Из этого следует, что кольцо и магнит обращены друг к другу одноимёнными полюсами, а векторы магнитной индукции (Вк и Вм) их полей направлены в противоположные стороны (рис. 125). Зная направление вектора индукции магнитного поля кольца, можно по правилу правой руки (см. рис. 97) определить направление индукционного тока в кольце. Отодвигаясь от приближающегося к нему магнита, кольцо противодействует увеличению проходящего сквозь него внешнего магнитного потока.
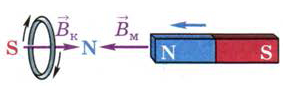
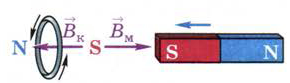
Рис. 125. Определение направления индукционного тока в кольце
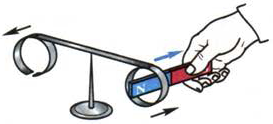
Рис. 126. При удалении магнита от сплошного кольца оно, притягиваясь, следует за магнитом
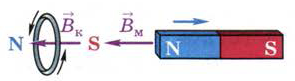
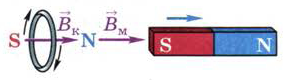
Рис. 127. Направление индукционного тока в кольце меняется при
изменении направления движения магнита относительно кольца
Теперь посмотрим, что произойдёт при уменьшении внешнего магнитного потока сквозь кольцо. Для этого, удерживая кольцо рукой, внесём в него магнит. Затем, отпустив кольцо, начнём удалять магнит. В этом случае кольцо будет следовать за магнитом, притягиваться к нему (рис. 126). Значит, кольцо и магнит обращены друг к другу разноимёнными полюсами, а векторы магнитной индукции их полей направлены в одну сторону (рис. 127). При одинаковом направлении Вк и Вм магнитное поле тока будет противодействовать уменьшению внешнего магнитного потока, проходящего сквозь кольцо.
Мы видим, что для определения направления индукционного тока прежде всего необходимо узнать, как направлен вектор магнитной индукции созданного этим током магнитного поля (в центре кольца). На основании результатов рассмотренных опытов (в одном из них внешний магнитный поток увеличивался, а в другом — уменьшался) было сформулировано правило, которое в современной формулировке звучит так:
возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует изменению внешнего магнитного потока, которое вызвало этот ток.
Данное правило было установлено в 1834 г. российским учёным Эмилием Христиановичем Ленцем, в связи с чем называется правилом Ленца.
1. Для чего проводился опыт, изображённый на рисунках 123 и 126?
2. Почему кольцо с разрезом не реагирует на приближение магнита?
3. Объясните явления, происходящие при приближении магнита к сплошному кольцу (см. рис. 125); при удалении магнита (см. рис. 127).
4. Как определить направление индукционного тока в кольце?
5. Сформулируйте правило Ленца.
1. Как вы думаете, почему прибор, изображённый на рис. 123, изготовлен из алюминия? Как проходил бы опыт, если бы прибор был железным; медным?
2. В данном ниже перечне логических операций, которые мы выполняли для определения направления индукционного тока, нарушена последовательность их проведения. Запишите в тетради буквы, обозначающие эти операции, расположив их в правильной последовательности.
а) Определили направление индукционного тока в кольце (пользуясь правилом правой руки).
б) Определили направление вектора индукции Вк магнитного поля тока в кольце по отношению к направлению вектора магнитной индукции Вм поля магнита, исходя из того, что кольцо отталкивается от магнита при его приближении (значит, они обращены друг к другу одноимёнными полюсами, и Вк ¯ Вм) и притягивается при удалении (значит, кольцо и магнит обращены друг к другу разноимёнными полюсами, и Вк Вм).
в) Определили направление вектора магнитной индукции Вм поля магнита (по расположению его полюсов).
Рассмотрим частный случай электромагнитной индукции: возникновение индукционного тока в катушке при изменении силы тока в ней.
Для этого проведём опыт, изображённый на рис. 128, а и схеме 128, б. При выполнении первой части опыта неоновая лампа JIH нам не понадобится, поэтому вынем её из патрона, оставив только две параллельные ветви: с реостатом Р и катушкой К. (Обратите внимание на условное обозначение катушки с сердечником на схеме 128, б и запомните его.)
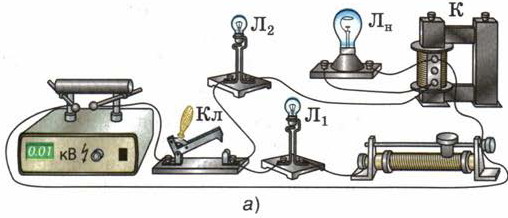
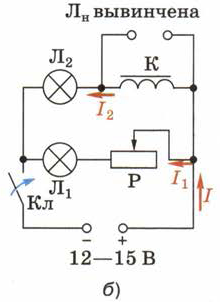
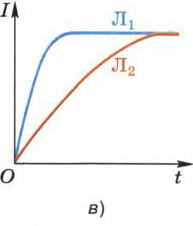
Рис. 128. Возникновение индукционного тока в катушке при изменении силы тока в ней при замыкании цепи
Замкнём цепь ключом Кл. Лампа Л1 загорится сразу, а Л2 — с опозданием приблизительно в 1 с. Причина запаздывания заключается в следующем. При замыкании цепи силы токов I, I1 и I2 (см. рис. 128, б) начинают расти. Благодаря этому увеличиваются индукции В1 и В2 магнитных полей (создаваемых этими же токами I1 и I2) и магнитные потоки Ф1 и Ф2, пронизывающие соответственно витки реостата и катушки. Получается, что проходящие сквозь реостат и катушку переменные потоки Ф1 и Ф2 создаются не внешними причинами (как было в опытах, рассмотренных в § 39), а благодаря изменению токов в самих этих устройствах.
Согласно явлению электромагнитной индукции, в реостате и в катушке возникают индукционные токи. Они препятствуют увеличению силы тока I1 и I2 (это следует из правила Ленца и правила правой руки). Но в катушке К индукционный ток будет значительно больше, чем в реостате Р, так как катушка имеет гораздо большее число витков и сердечник, т. е. обладает большей индуктивностью, чем реостат.
Индуктивность (коэффициент самоиндукции) — это физическая величина, введённая для оценивания способности катушки противодействовать изменению силы тока в ней. Индуктивность L катушки зависит от её формы, размеров, числа витков и наличия или отсутствия сердечника (например, железного). Единица индуктивности в СИ — генри (Гн).
Чем больше сила индукционного тока, тем большее противодействие он оказывает изменению силы тока, созданного источником. Поэтому ток в ветви с катушкой возрастает медленнее, чем в ветви с реостатом, и лампа Л2 загорается с опозданием (рис. 128, в).
Теперь посмотрим, что будет происходить при размыкании цепи. Для этого неоновую лампу Лн поместим в патрон, а лампу Л1 вывинтим, разомкнув тем самым участок цепи с реостатом (рис. 129).
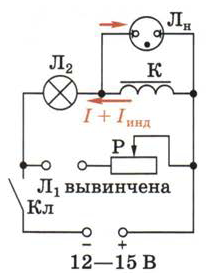
Рис. 129. Демонстрация явления самоиндукции при размыкании цепи
При замыкании цепи загорится только лампа Л2. Неоновая лампа не включается потому, что напряжение, необходимое для её зажигания, значительно больше напряжения, подаваемого от источника тока.
Теперь разомкнём цепь — лампа накаливания гаснет, зато неоновая даёт яркую кратковременную вспышку. Значит, уменьшение тока при размыкании цепи создаёт настолько мощный индукционный ток, противодействующий уменьшению тока в катушке, что напряжение на ней оказывается достаточным для зажигания лампы (и значительно превышающим напряжение источника!).
В проделанном опыте мы наблюдали явление самоиндукции.
Явление самоиндукции заключается в возникновении индукционного тока в катушке при изменении силы тока в ней. При этом возникающий индукционный ток называется током самоиндукции.
Конечно, ток самоиндукции возникает не только в катушках, но и в любых других проводниках, если сила тока изменяется. Но, как уже отмечалось, в катушках с относительно небольшим числом витков, не имеющих сердечника, и тем более в прямых проводниках (т. е. в элементах цепи, обладающих малой индуктивностью) ток самоиндукции обычно невелик и не оказывает существенного влияния на процессы в электрической цепи.
Появление мощного индукционного тока при размыкании цепи свидетельствует о том, что магнитное поле тока в катушке обладает энергией. Именно за счёт уменьшения энергии магнитного поля совершается работа по созданию индукционного тока. А накопилась эта энергия раньше, при замыкании цепи, когда за счёт энергии источника тока совершалась работа по преодолению тока самоиндукции, препятствующего увеличению тока в цепи, и его магнитного поля.
Энергия магнитного поля тока определяется по формуле
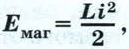
где L — индуктивность проводника, i — сила тока в этом проводнике.
1. Какое явление изучалось на опыте, представленном на рисунках 128 и 129?
2. Расскажите о ходе каждой части опыта. Объясните наблюдаемые явления.
3. В чём заключается явление самоиндукции?
4. Может ли возникнуть ток самоиндукции в прямом проводнике
с током? Если нет, то объясните почему; если да, то при каком условии.
5. За счёт уменьшения какой энергии совершалась работа по созданию индукционного тока при размыкании цепи?
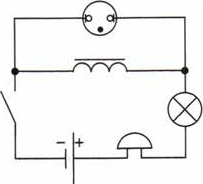
Рис. 130
В электрической цепи (рис. 130) напряжение, получаемое от источника тока, меньше напряжения зажигания неоновой лампы.
Как будет себя вести неоновая лампа при замыкании и размыкании ключа?
Что будет происходить с каждым элементом цепи (исключая источник тока и ключ) при замкнутом ключе; при замыкании ключа; при размыкании ключа?
Рассмотрим ещё раз получение индукционного тока в катушке с помощью перемещения относительно неё постоянного магнита (см. рис. 119, а). Но теперь будем периодически двигать магнит вверх и вниз в течение нескольких секунд. Мы увидим, что при этом стрелка гальванометра отклоняется от нулевого деления то в одну, то в другую сторону. Это говорит о том, что модуль силы индукционного тока в катушке и направление этого тока периодически меняются.
Электрический ток, периодически меняющийся со временем по модулю и направлению, называется переменным током.
В осветительной сети наших домов и во многих отраслях промышленности используется именно переменный ток.
В настоящее время для получения переменного тока используют в основном электромеханические индукционные генераторы, т. е. устройства, в которых механическая энергия преобразуется в электрическую. Индукционными они называются потому, что их действие основано на явлении электромагнитной индукции.
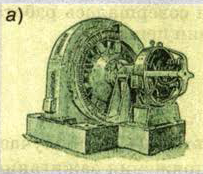

Генератор переменного тока:
а — внешний вид; б — общий вид на электростанции вместе с паровой турбиной,
приводящей ротор генератора во вращение.

Рис. 131. Схема генератора переменного тока
В § 39 рассматривался пример получения индукционного тока в плоском контуре при вращении внутри него магнита (см. рис. 121, б). На этом принципе и работает электромеханический генератор переменного тока. Неподвижная часть генератора, аналогичная контуру, называется статором, а вращающаяся, т. е. магнит, — ротором. В мощных промышленных генераторах вместо постоянного магнита используется электромагнит.
Статор промышленного генератора представляет собой стальную станину цилиндрической формы (станина — это основная несущая часть машины, на которой монтируются различные рабочие узлы, механизмы и пр.). Во внутренней его части прорезаются пазы, в которые витками укладывается толстый медный провод. В витках и индуцируется переменный электрический ток при изменении пронизывающего их магнитного потока.
Магнитное поле создаётся ротором (рис. 131, а). Он представляет собой электромагнит: на стальной сердечник сложной формы надета обмотка, по которой протекает постоянный электрический ток. Ток к этой обмотке подводится через щётки и кольца от постороннего источника постоянного тока.
На рис. 131, б приведена схема генератора переменного тока. Штрихами показано примерное расположение линий индукции магнитного поля ротора. При вращении ротора какой-либо внешней механической силой создаваемое им магнитное поле тоже вращается. При этом магнитный поток, пронизывающий витки обмотки статора, периодически меняется, в результате чего в них индуцируется переменный ток.
а)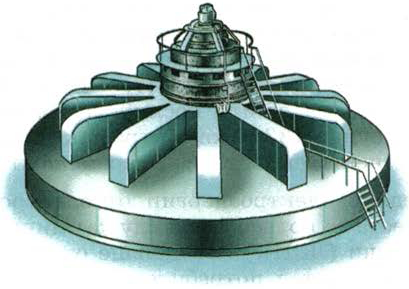 б)
б)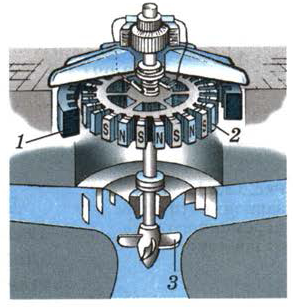
Рис. 132. Внешний вид и устройство мощного гидрогенератора
На тепловых электростанциях ротор генератора вращается с помощью паровой турбины, на гидроэлектростанциях — с помощью водяной турбины.
На рис. 132, а изображён внешний вид мощного гидрогенератора, а на рис. 132, б схематично показано его устройство, где цифрой 1 обозначен статор, цифрой 2 — ротор, а цифрой 3 — водяная турбина.
Ротор гидрогенератора имеет не одну, а несколько пар магнитных полюсов. Чем больше пар полюсов, тем больше частота переменного электрического тока, вырабатываемого генератором при данной скорости вращения ротора. Поскольку скорость вращения водяных турбин обычно невелика, то для создания тока стандартной частоты используют многополюсные роторы.
Стандартная частота переменного тока, применяемого в промышленности и осветительной сети в России и многих других странах, равна 50 Гц. Это означает, что на протяжении 1 с ток 50 раз течёт в одну сторону и 50 раз в другую (Рис. 133). В некоторых странах (например, США) стандартная частота переменного тока равна 60 Гц.
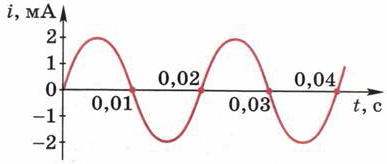
Рис. 133. График зависимости силы переменного тока от времени.
Амплитуда тока - 2 мА, период одного колебания тока - 0,02 с.
 |
 |
| Современные высоковольтные ЛЭП | Первые ЛЭП |
Сила тока, вырабатываемого генераторами переменного тока, меняется со временем по гармоническому закону (т. е. по закону синуса или косинуса - то есть так: i(t) = imax×sin(wt + j), где Imax - амплитуда тока, А, w - круговая частота, с-1, j - начальная фаза, радиан). На рис. 133 показан график изменения силы тока i со временем t.
Для передачи электроэнергии от электростанций в места её потребления служат линии электропередачи (ЛЭП). Чем дальше от электростанции находится потребитель тока, тем больше энергии Q тратится на нагревание проводов и тем меньше доходит до потребителя:
![]()
Уменьшение потерь электроэнергии при её передаче от электростанций к потребителям является важной задачей экономики.
Из закона Джоуля—Ленца (Q = I2Rt) следует, что уменьшить потери можно за счёт уменьшения сопротивления R проводов и силы тока I в них (что более эффективно, поскольку при уменьшении I в n раз Q уменьшается в n2 раз).
Сопротивление проводов будет тем меньше, чем больше площадь S их поперечного сечения и чем меньше удельное сопротивление r металла, из которого они изготовлены так как R = r (l /S).
Провода делают из меди или алюминия, так как среди относительно недорогих металлов они обладают наименьшим удельным сопротивлением. Увеличивать толщину проводов экономически невыгодно (ввиду увеличения расхода металла) и неудобно (из-за трудностей при их подвеске).
Поэтому существенного снижения потерь Q можно добиться только за счёт уменьшения силы тока I. Но при этом необходимо во столько же раз увеличить получаемое от генератора напряжение U, чтобы не снижать мощность тока Р (так как Р = UI).
(Здесь U, I — так называемые действующие значения напряжения и силы переменного тока. Они равны соответственно напряжению и силе постоянного тока, выделяющего в проводнике ежесекундно столько же тепла, что и переменный ток. Действующие значения напряжения и силы переменного тока в корень из двух раз меньше амплитудных:
).
Без такого преобразования силы тока и напряжения передача электроэнергии на большие расстояния становится невыгодной из-за существенных потерь.
ПАВЕЛ
НИКОЛАЕВИЧ ЯБЛОЧКОВ
(1847—1894)
Русский электротехник и изобретатель. Изобрёл дуговую лампу («свеча Яблочкова»), сконструировал первый генератор переменного тока, трансформатор, сделал изобретения в области электрических машин и химических источников тока
Решение этой важнейшей технической задачи стало возможным только после изобретения трансформатора — устройства, предназначенного для увеличения или уменьшения переменного напряжения и силы тока.
Трансформатор был изобретён в 1876 г. русским учёным Павлом Николаевичем Яблочковым. В основе его работы лежит явление электромагнитной индукции. На рис. 134, а показан внешний вид трансформатора, а на рис. 134,б схематично изображены его основные части. Обратите внимание на то, что число витков в обмотках различно: в данном случае N2 > N1. Протекающий в первичной обмотке переменный ток создаёт (главным образом в сердечнике) переменное магнитное поле, которое, в свою очередь, порождает переменное электрическое поле. В результате действия этого поля на концах вторичной обмотки возникает переменное напряжение U2.

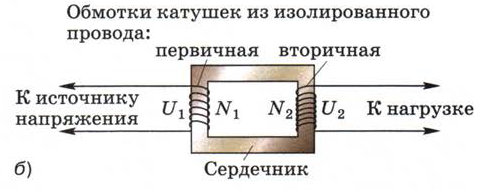
Рис. 134. Внешний вид и схема устройства повышающего трансформатора
Величина U2 определяется из соотношения:
Значит, при N2 > N1 трансформатор будет повышающим (так как U2 > U1), а при N2< N1 — понижающим (в данном случае U2 < U1).
Теперь вернёмся к вопросу о передаче электроэнергии от электростанции к месту её потребления. Напряжение, вырабатываемое генератором, обычно не превышает 25 кВ. А для оптимальной передачи электроэнергии на большие расстояния требуется напряжение порядка сотен киловольт. Поэтому ток с электростанции сначала подаётся на расположенную неподалёку повышающую трансформаторную подстанцию, где напряжение повышается до нескольких сотен киловольт (в большинстве случаев оно не превышает 750 кВ), и под таким напряжением подаётся в ЛЭП. Поскольку такое высокое напряжение не может быть предложено потребителю, то в конце линии его подают поочерёдно на несколько трансформаторных подстанций, понижающих напряжение до 380 или 220 В, а затем — на предприятия или в жилые дома.
Внеешний вид силового масляного трансформатора
Трансформаторы нашли широкое применение в быту. Например, при подзарядке сотового телефона имеющийся в зарядном устройстве трансформатор понижает напряжение, полученное из осветительной сети и равное 220 В, до 5,5 В, пригодного для телефона. В телевизоре имеется несколько трансформаторов (как понижающих, так и повышающих), поскольку для питания различных его узлов требуется напряжение от 1,5 В до 25 кВ.
1. Какой электрический ток называется переменным? С помощью какого простого опыта его можно получить?
2. Где используют переменный электрический ток?
3. Расскажите об устройстве и принципе действия промышленного генератора.
4. Чем приводится во вращение ротор генератора на тепловой электростанции; на гидроэлектростанции?
5. Почему в гидрогенераторах используют многополюсные роторы?
6. По какому физическому закону можно определить потери электроэнергии в ЛЭП и за счёт чего их можно уменьшить?
7. Для чего при уменьшении силы тока во столько же раз повышают его напряжение перед подачей в ЛЭП?
8. Расскажите об устройстве, принципе действия и применении трансформатора.
1. Электростанции России вырабатывают переменный ток частотой 50 Гц. Определите период этого тока.
2*. По графику (см. рис. 133) определите период, частоту и амплитуду колебаний силы тока
i.
Явление электромагнитной индукции было открыто Фарадеем в 1831 г.
В том же году в Англии родился Джеймс Максвелл, ставший впоследствии учёным и сделавший важнейшее научное открытие, которое позволило глубже понять сущность явления электромагнитной индукции.

ДЖЕЙМС МАКСВЕЛЛ
(1831-1879)
Английский физик. Теоретически предсказал существование электромагнитных волн,определил, что в вакууме они должны распространяться со скоростью света. Создал теорию электромагнитного поля
Напомним, что согласно явлению электромагнитной индукции при изменении магнитного потока, пронизывающего контур замкнутого проводника, в этом проводнике возникает индукционный ток. Но ток может возникнуть только при наличии электрического поля.
Предположение о возникновении электрического поля в результате изменения магнитного сразу вызвало у учёных ряд вопросов. Например: отличается ли оно от поля, созданного неподвижными электрическими зарядами?
Возникает ли это поле только в проводнике или существует и в пространстве вокруг него? Играет какую-либо роль в возникновении электрического поля замкнутый проводник, по которому протекает индукционный ток, или оно существует в пространстве независимо от наличия проводника?
Ответы на эти и другие вопросы были получены в 1865 г., когда Максвелл создал теорию электромагнитного поля. Он теоретически доказал, что всякое изменение со временем магнитного поля приводит к возникновению переменного электрического поля, а всякое изменение со временем электрического поля порождает переменное магнитное поле.
Эти порождающие друг друга переменные электрическое и магнитное поля образуют единое электромагнитов поле.
Источником электромагнитного поля служат ускоренно движущиеся электрические заряды.
Если электрические заряды движутся с ускорением, например колеблются, то создаваемое ими электрическое поле периодически меняется. Переменное электрическое поле создаёт в пространстве переменное магнитное поле, которое, в свою очередь, порождает переменное электрическое и т. д.
Переменное электрическое поле называется вихревым, поскольку его силовые линии замкнуты подобно линиям индукции магнитного поля. Это отличает его от поля электростатического (т. е. постоянного, не меняющегося во времени), которое существует вокруг неподвижных заряженных тел. Силовые линии электростатического поля начинаются на положительных зарядах и заканчиваются на отрицательных.
Открытие электромагнитного поля позволило более детально описать механизм возникновения индукционного тока. Во всех опытах по получению индукционного тока (см. § 39) тем или иным образом изменялся магнитный поток, пронизывающий контур замкнутого проводника. При этом, согласно теории Максвелла, возникало вихревое электрическое поле, под действием которого свободные заряды, всегда имеющиеся в проводнике, приходили в направленное движение. В данном случае проводник, замкнутый на гальванометр, играл лишь роль индикатора, обнаруживающего возникшее в данной области пространства электрическое поле. Электрическое поле существует независимо от наличия проводника.
Созданная Максвеллом теория, позволившая предсказать существование электромагнитного поля за 22 года до того, как оно было обнаружено экспериментально, считается величайшим из научных открытий, роль которого в развитии науки и техники трудно переоценить.
1. Кем и когда была создана теория электромагнитного поля и в чём заключалась её суть?
2. Что служит источником электромагнитного поля?
3 Чем отличаются силовые линии вихревого электрического поля от силовых линий электростатического?
4. Опишите механизм возникновения индукционного тока, опираясь на знание о существовании электромагнитного поля.
В опыте, изображённом на рис. 120, при замыкании ключа сила тока, протекающего через катушку А, в течение некоторого промежутка времени увеличивалась. При этом в цепи катушки С возникал кратковременный ток. Отличаются ли чем-нибудь электрические поля, под действием которых возникали токи в катушках А и С? Существовали бы эти поля в момент замыкания ключа, если бы не было катушки С с гальванометром?
Из созданной Максвеллом теории можно сделать вывод о том, что быстропеременное электромагнитное поле должно распространяться в пространстве в виде поперечных волн. Причём эти волны могут существовать не только в веществе, но и в вакууме. Опираясь исключительно на теоретические выводы, Максвелл определил также, что электромагнитные волны должны распространяться в вакууме со скоростью 300 000 км/с, т. е. со скоростью света (скорость света, как известно, была измерена задолго до этого).
Вы уже знаете, что в механических волнах, например в звуковых, энергия передаётся от одних частиц среды к другим. При этом частицы приходят в колебательное движение, т. е. их смещение от положения равновесия периодически меняется. Для передачи звука обязательно нужна вещественная среда.
В связи с тем, что электромагнитные волны распространяются в веществе и в вакууме, возникает вопрос: что совершает колебания в электромагнитной волне, т. е. какие физические величины периодически меняются в ней?
Электромагнитная волна представляет собой систему порождающих друг друга и распространяющихся в пространстве переменных электрического и магнитного полей.
Напомним, что количественной характеристикой магнитного поля является вектор магнитной индукции В.
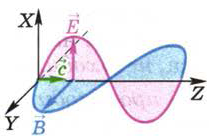
Рис. 135. Модель электромагнитной волны:
Е — напряжённость электрического поля,
В — индукция магнитного поля;
с — скорость волны.
Основной количественной характеристикой электрического поля служит векторная величина, называемая напряжённостью электрического поля, которая обозначается символом Е. Напряжённость Е электрического поля в какой-либо его точке равна отношению силы F, с которой поле действует на точечный положительный заряд, помещённый в эту точку, к значению этого заряда q.
Когда говорят, что магнитное и электрическое поля меняются, то это означает, что меняются соответственно вектор индукции магнитного поля В и вектор напряжённости электрического поля Е.
В электромагнитной волне именно векторы В и Е периодически меняются по модулю и по направлению, т. е. колеблются.
На рис. 135 изображены вектор напряжённости электрического поля Е и вектор индукции магнитного поля В электромагнитной волны в один и тот же момент времени. Это как бы «моментальный снимок» волны, распространяющейся в направлении оси Z. Плоскость, проведённая через векторы В и Е в любой точке, перпендикулярна направлению распространения волны, что говорит о поперечности волны.
За время, равное периоду колебаний, волна переместится вдоль оси Z на расстояние, равное длине волны. Для электромагнитных волн справедливы те же соотношения между длиной волны l, её скоростью с, периодом Т и частотой n колебаний, что и для механических волн:
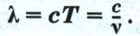
Максвелл не только научно обосновал возможность существования электромагнитных волн, но и указал, что для создания интенсивной электромагнитной волны, которую можно было бы зарегистрировать приборами на некотором расстоянии от источника, необходимо, чтобы колебания векторов В и Е происходили с достаточно высокой частотой (порядка 100000 колебаний в секунду и больше).
В 1888 г. немецкому учёному Генриху Герцу удалось получить и зарегистрировать электромагнитные волны. В результате опытов Герца были также обнаружены все свойства электромагнитных волн, теоретически предсказанные Максвеллом.
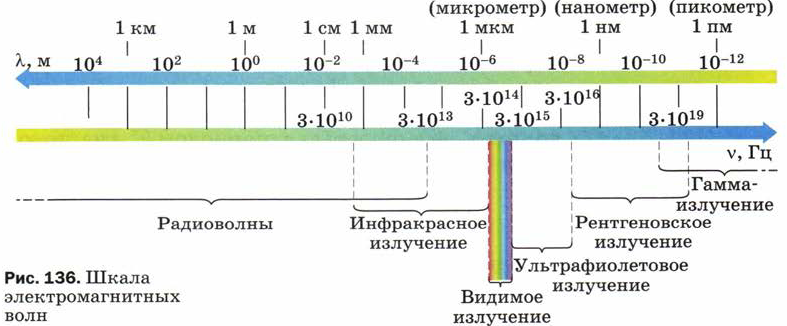
Всё окружающее нас пространство буквально пронизано электромагнитными волнами различных частот. В настоящее время все электромагнитные волны разделены по длинам волн (и соответственно по частотам) на шесть основных диапазонов, которые представлены на рис. 136.
Границы диапазонов весьма условны, поэтому, как видно из рисунка, в большинстве случаев соседние диапазоны несколько перекрывают друг друга.
Электромагнитные волны разных частот отличаются друг от друга проникающей способностью, скоростью распространения в веществе, видимостью, цветностью и некоторыми другими свойствами.

ГЕНРИХ ГЕРЦ
(1857-1894)
Немецкий физик, один из основоположников электродинамики. Экспериментально доказал существование электромагнитных волн
Они могут оказывать как положительное, так и отрицательное воздействие на живые организмы. Например, инфракрасное, т. е. тепловое, излучение играет определяющую роль в поддержании жизни на Земле, поскольку люди, животные и растения могут существовать и нормально функционировать только при определённых температурах.
Видимый свет даёт нам информацию об окружающем мире и возможность ориентироваться в пространстве. Он необходим также для протекания процесса фотосинтеза в растениях, в результате чего выделяется кислород, необходимый для дыхания живых организмов.
Влияние на человека ультрафиолетового излучения (вызывающего загар) в большой степени определяется интенсивностью и продолжительностью облучения. В допустимых дозах оно повышает сопротивляемость организма человека к различным заболеваниям, в частности инфекционным. Превышение допустимой дозы может вызвать ожоги кожи, развитие онкологических заболеваний, ослабление иммунитета, повреждение сетчатки глаз. Глаза можно защитить с помощью стеклянных очков (как тёмных, так и прозрачных, но не пластиковых), так как стекло поглощает значительную часть ультрафиолетовых лучей.
Вы знакомы и с рентгеновским излучением, в частности с его широким применением в медицине — флюорографическое обследование или рентгеновский снимок наверняка делали каждому из вас. Но слишком большие дозы или частые обследования с помощью рентгеновских лучей могут вызвать серьёзные заболевания.
Получение электромагнитных волн имеет огромное научное и практическое значение. В этом можно убедиться на примере всего лишь одного диапазона — радиоволн, применяемых для телевизионной и радиосвязи, в радиолокации (т. е. для обнаружения объектов и измерения расстояния до них), в радиоастрономии и других сферах деятельности.
1. Какие выводы относительно электромагнитных волн можно
сделать из теории Максвелла?
2. Какие физические величины периодически меняются в электромагнитной волне?
3. Какие соотношения между длиной волны, её скоростью, периодом и частотой
колебаний справедливы для электромагнитных волн?
4. При каком условии волна будет достаточно интенсивной для того, чтобы её можно
было зарегистрировать?
5. Когда и кем были впервые получены электромагнитные волны?
6. Приведите примеры применения разных диапазонов электромагнитных волн и их
воздействия на живые организмы.
1. На какой частоте суда передают сигнал бедствия SOS, если по международному соглашению длина радиоволны должна быть 600 м?
2. Радиосигнал, посланный с Земли на Луну, может отразиться от поверхности Луны и вернуться на Землю. Предложите способ измерения расстояния между Землёй и Луной с помощью радиосигнала.
Указание: задача решается таким же методом, каким измеряется глубина моря с помощью эхолокации (см. § 30).
3. Можно ли измерить расстояние между Землёй и Луной с помощью звуковой или ультразвуковой волны? Ответ обоснуйте.
Радиовещание (т. е. передача звуковой информации на большие расстояния) осуществляется посредством электромагнитных волн, излучаемых антенной радиопередающего устройства. Напомним, что источником электромагнитных волн являются ускоренно движущиеся заряженные частицы. Значит, для того чтобы антенна излучала электромагнитные волны, в ней нужно возбуждать колебания свободных электронов. Такие колебания называются электромагнитными (поскольку они порождают электромагнитное поле, распространяющееся в пространстве в виде электромагнитных волн).
Для создания мощной электромагнитной волны, которую можно было бы зарегистрировать приборами на больших расстояниях от излучающей её антенны, необходимо, чтобы частота волны была не меньше 0,1 МГц (105 Гц).(Дальность распространения волны зависит от её мощности Р, а мощность — от частоты v: Р - v4. Из этой зависимости следует, что уменьшение частоты волны, например, всего лишь в 2 раза приведёт к уменьшению её мощности в 16 раз и соответствующему уменьшению дальности распространения.)
Колебания таких больших частот невозможно получить от генератора переменного электрического тока. Поэтому они подаются на антенну от генератора высокочастотных электромагнитных колебаний, имеющегося в каждом радиопередающем устройстве.
Одной из основных частей генератора является колебательный контур — колебательная система, в которой могут существовать свободные электромагнитные колебания. Колебательный контур состоит из конденсатора (или батареи конденсаторов) и проволочной катушки.
Получить свободные электромагнитные колебания и удостовериться в их существовании можно с помощью установки, изображённой на рис. 137.
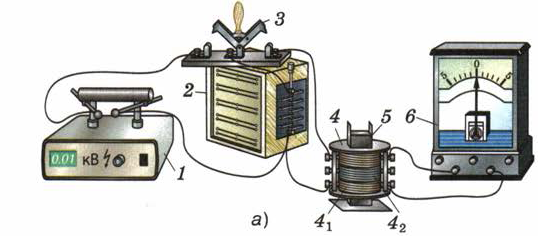
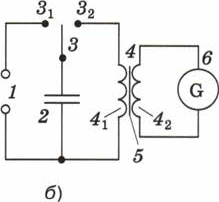
Рис. 137. Установка для получения свободных электромагнитных колебаний.
Катушка 4 с сердечником 5 (рис. 137, а) состоит из двух обмоток: первичной 41, (из 3600 витков) и вторичной 42 (расположенной поверх первичной в средней её части и имеющей 40 витков).
Первичная обмотка катушки и батарея конденсаторов 2, соединённые друг с другом через переключатель 3, составляют колебательный контур. Вторичная обмотка замкнута на гальванометр 6, который будет регистрировать возникновение колебаний в контуре.
Поставим переключатель в положение 31 (рис. 137, б), соединив батарею конденсаторов с источником постоянного тока 1. Батарея зарядится от источника. Перекинем переключатель в положение 32, соединив батарею с катушкой. При этом стрелка гальванометра совершит несколько затухающих колебаний, отклоняясь от нулевого деления то в одну, то в другую сторону, и остановится на нуле.
Чтобы объяснить наблюдаемое явление, обратимся к рисунку 138. Пусть при зарядке от источника тока (переключатель в положении 31) конденсатор получил некоторый максимальный заряд qm. Допустим, при этом верхняя его обкладка зарядилась положительно, а нижняя — отрицательно (рис. 138, а). Между обкладками возникло напряжение Um и электрическое поле, обладающее энергией Еэл m.
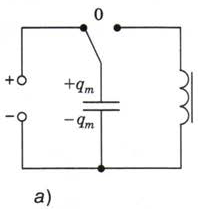
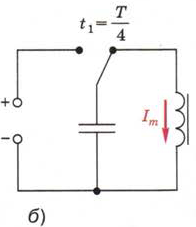
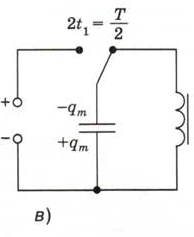
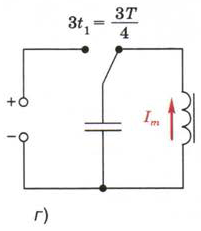
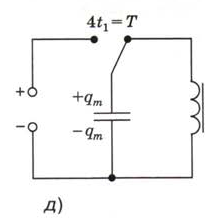
Рис. 138. Объяснение возникновения и существования электромагнитных колебаний в колебательном контуре
При замыкании на катушку (переключатель в положении 32) в момент, который примем за начало отсчёта времени, конденсатор начинает разряжаться, и в контуре появляется электрический ток. Сила тока увеличивается постепенно, так как возникший в катушке ток самоиндукции направлен против тока, созданного разряжающимся конденсатором.
Через некоторый промежуток времени t1 от начала разрядки конденсатор полностью разрядится — его заряд, напряжение между обкладками и энергия электрического поля будут равны нулю (рис. 138, б). Но, согласно закону сохранения энергии, энергия электрического поля не исчезла — она перешла в энергию магнитного поля тока катушки, которая в этот момент достигает максимального значения Емаг m. Наибольшему значению энергии соответствует и наибольшая сила тока Im.
Поскольку конденсатор разряжен, сила тока в контуре начинает уменьшаться. Но теперь ток самоиндукции направлен в ту же сторону, что и ток разряжавшегося конденсатора, и препятствует его уменьшению. Благодаря току самоиндукции к моменту времени 2t1 от начала разрядки конденсатор перезарядится: его заряд вновь будет равен qm, но теперь верхняя обкладка будет заряжена отрицательно, а нижняя — положительно (рис. 138, в).
Понятно, что через промежуток времени, равный 3t1 , конденсатор вновь будет разряжен (рис. 138, г), а через 4t1 будет заряжен так же, как в момент начала разрядки (рис. 138, д).
За промежуток времени, равный 4t1 произошло одно полное колебание. Значит, Т = 4t1 , где Т — период колебаний (a t1 , 2t1, 3t1 — соответственно четверть, половина и три четверти периода).
При периодическом изменении в катушке 4Х силы тока и его направления соответственно меняется и создаваемый этим током магнитный поток, пронизывающий катушку 42. При этом в ней возникает переменный индукционный ток, регистрируемый гальванометром. Исходя из того что стрелка гальванометра совершила несколько затухающих колебаний и остановилась на нуле, можно сделать вывод, что электромагнитные колебания тоже были затухающими. Энергия, полученная контуром от источника тока, постепенно расходовалась на нагревание проводящих частей контура. Когда запас энергии иссяк, колебания прекратились.
Напомним, что колебания, происходящие только благодаря начальному запасу энергии, называются свободными. Период свободных колебаний равен собственному периоду колебательной системы, в данном случае периоду колебательного контура. Формула для определения периода свободных электромагнитных колебаний была получена английским физиком Уильямом Томсоном в 1853 г. Она называется формулой Томсона и выглядит так:
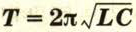
Из данной формулы следует, что период колебательного контура определяется параметрами составляющих его элементов: индуктивностью катушки и ёмкостью конденсатора. Например, при уменьшении ёмкости или индуктивности период колебаний должен уменьшиться, а их частота — увеличиться. Проверим это на опыте. Уменьшим ёмкость батареи, отключив от неё несколько конденсаторов. Мы увидим, что колебания стрелки гальванометра участились.
В начале параграфа отмечалось, что подаваемые в антенну высокочастотные колебания необходимы для создания электромагнитных волн. Но для того чтобы волна излучалась в течение длительного времени, нужны незатухающие колебания. Для создания в контуре незатухающих колебаний необходимо восполнять потери энергии, периодически подключая конденсатор к источнику тока. В генераторе это осуществляется автоматически.
1. Для чего электромагнитные волны подаются в антенну?
2. Почему в радиовещании используются электромагнитные волны высокой частоты?
3. Что представляет собой колебательный контур?
4. Расскажите о цели, ходе и наблюдаемом результате опыта, изображённого на рис. 137. Каким образом гальванометр мог регистрировать происходящие в этом контуре колебания?
5. Какие преобразования энергии происходят в результате электромагнитных колебаний?
6. Почему ток в катушке не прекращается в тот момент, когда конденсатор разряжен?
7. От чего зависит собственный период колебательного контура? Как его можно изменить?
Колебательный контур состоит из конденсатора переменной ёмкости и катушки. Как получить в этом контуре электромагнитные колебания, периоды которых отличались бы в 2 раза?
Передача и приём информации посредством электромагнитных волн называется радиосвязью. Линии радиосвязи используют, например, для осуществления радиотелефонной связи, передачи телеграмм, факсимиле (факсов), радиовещательных и телевизионных программ.
Радиосвязь представляет собой довольно сложный процесс. Поэтому рассмотрим лишь наиболее общие принципы одного из её видов — радиотелефонной связи, т. е. передачи звуковой информации, например речи и музыки, с помощью электромагнитных волн.
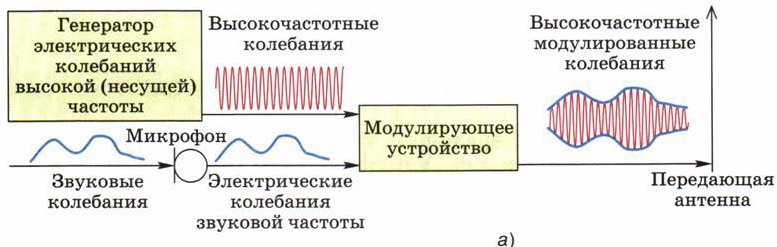
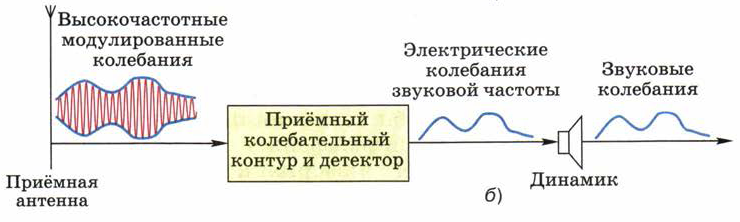
Рис. 139. Блок-схема процесса радиосвязи
Для получения целостного представления об этом процессе обратимся к блок-схеме, представленной на рис. 139.
На рис. 139, а изображено передающее устройство, состоящее из генератора высокочастотных колебаний, микрофона, модулирующего устройства и передающей антенны.
В микрофон поступают звуковые колебания (речь, музыка и т. д.). Они преобразуются микрофоном в электрические колебания такой же формы, какую имеют звуковые. Из микрофона низкочастотные электрические колебания поступают в модулирующее устройство. Туда же из генератора подаются высокочастотные колебания постоянной амплитуды.
В модулирующем устройстве амплитуду высокочастотных колебаний изменяют (модулируют) с помощью электрических колебаний звуковой частоты. В результате амплитуда становится переменной, причём меняется она точно так же, как и поступающие из микрофона электрические колебания. Такие высокочастотные модулированные по амплитуде колебания несут в себе информацию о форме звукового сигнала. Поэтому частота высокочастотных колебаний называется несущей.
Процесс изменения амплитуды высокочастотных колебаний с частотой, равной частоте звукового сигнала, называется амплитудной модуляцией.
Под воздействием высокочастотных модулированных колебаний в передающей антенне возникает переменный ток высокой частоты. Этот ток порождает в пространстве вокруг антенны электромагнитное поле, которое распространяется в пространстве в виде электромагнитных волн и достигает антенн радиоприёмных устройств.
Вы уже знаете о том, что мощность электромагнитной волны пропорциональна четвёртой степени её частоты: Р ~ v4.
Электромагнитные волны звуковых, т. е. низких, частот (от 16 до 20 ООО Гц) имеют малую мощность и после излучения очень быстро затухают. Этим и вызвана необходимость использования модулированных радиоволн, которые благодаря высокой несущей частоте распространяются на большие расстояния и при этом содержат информацию о форме передаваемых звуковых колебаний.
Как видно из рисунка 139, б, радиоприёмное устройство состоит из приёмной антенны, приёмного резонирующего колебательного контура и детектора — элемента, пропускающего переменный ток только в одном направлении.
В приёмную антенну поступают волны от множества радиостанций. Но каждая радиостанция осуществляет вещание только на строго определённой, отведённой ей несущей частоте.
Настраивая свой радиоприёмник на частоту нужной радиостанции, вы меняете собственную частоту имеющегося в приёмнике колебательного контура так, чтобы она была равна несущей частоте данной радиостанции, т. е. чтобы контур был настроен в резонанс с колебаниями, генерируемыми на данной радиостанции. При этом амплитуда колебаний выбранной радиостанции в контуре вашего приёмника будет максимальной по сравнению с амплитудами колебаний, поступивших от радиостанций, вещающих на других несущих частотах. В этом заключается второе назначение несущей частоты — она обеспечивает возможность настройки на частоту нужной радиостанции.
Рис. 140. Графики высокочастотных модулированных колебаний и звуковых колебаний

АЛЕКСАНДР СТЕПАНОВИЧ ПОПОВ
(1859—1906)
Русский физик, электротехник, изобретатель радио. Сконструировал генератор электромагнитных колебаний. Изобрёл приёмную антенну, построил первый в мире радиоприёмник
Принятые колебания сначала усиливают. Затем для преобразования высокочастотных модулированных колебаний в звуковые производят детектирование, т. е. процесс, обратный модуляции. Детектирование проводится в два этапа: сначала с помощью детектора (представляющего собой элемент с односторонней проводимостью) из высокочастотных модулированных колебаний получают высокочастотный пульсирующий ток (рис. 140, а), а затем в динамике этот ток сглаживается и преобразуется в колебания звуковых частот (рис. 140, б). На возможность использования электромагнитных волн для передачи радиосигналов ...
Радиосигналы — электромагнитные волны, излучаемые в течение коротких промежутков времени в диапазоне частот от 104 Гц до 1010 кГц.
... впервые указал в 1889 г. Александр Степанович Попов. В 1896 г. при помощи сконструированных им передатчика и приёмника радиосигналов передал первую в мире радиограмму, состоящую из двух слов «Генрих Герц».
При передаче телевизионных программ высокочастотные колебания модулируются не только звуковым, но и видеосигналом. Это осуществляется с помощью телевизионной передающей трубки, которая преобразует оптическое изображение в электромагнитные колебания. Модулированные таким образом высокочастотные колебания заключают в себе информацию и о звуке, и об изображении.
В телевидении используются более высокие (порядка миллиардов герц) несущие частоты.
1. Что называется радиосвязью?
2. Приведите 2-3 примера использования линий радиосвязи.
3. Используя рисунки 139 и 140, расскажите о принципах осуществления радиотелефонной связи.
4. Частота каких колебаний называется несущей?
5. В чём заключается процесс амплитудной модуляции электрических колебаний?
6. Почему в радиосвязи не используются электромагнитные волны звуковых частот?
7. В чём заключается процесс детектирования колебаний?
Период колебаний зарядов в антенне, излучающей радиоволны, равен 10”7 с. Определите частоту этих радиоволн.
В начале XIX в. опытным путём была подтверждена справедливость гипотезы о волновой природе света. В то время ни о каких волнах, кроме механических, учёные ещё не знали. Поэтому считали, что свет, подобно звуку, представляет собой механическую упругую волну.
Вы уже знаете, что упругие волны могут возникать только в веществе, поскольку именно частицы вещества совершают упругие колебания, распространяющиеся в пространстве (вспомните опыт, доказывающий, что звук не распространяется в вакууме).
Значит, если свет — упругая волна, то для его распространения нужна среда.
Однако свет от звёзд доходит до нас через такие области космического пространства, где нет вещества. Учитывая этот факт, сторонники волновых воззрений на природу света выдвинули гипотезу о том, что всё мировое пространство заполнено некой невидимой упругой средой, которую они назвали светоносным эфиром (идея о существовании эфира была высказана ещё в XVII в.). Считалось, что именно в этом эфире и распространяется свет.

МАКС ПЛАНК
(1858-1947)
Немецкий физик-теоретик, основоположник квантовой физики.
Закон излучения М.Планка явился основой нового этапа развития физики
В то же время предположение о существовании светоносного эфира порождало много противоречий и вопросов. Так, например, в конце второго десятилетия XIX в. было выяснено, что свет является поперечной волной. Известно, что упругие поперечные волны возникают только в твёрдых телах. Получалось, что светоносный эфир представляет собой твёрдое тело.
В связи с этим возникал вопрос о том, как планеты и другие небесные тела могут двигаться сквозь твёрдый эфир, не испытывая при этом никакого сопротивления.
Во второй половине XIX в. Максвелл создал теорию электромагнитного поля, согласно которой электромагнитные волны, подобно световым, являются поперечными и распространяются в вакууме со скоростью света. Исходя из того, что световые и электромагнитные волны обладают общими свойствами, Максвелл предположил, что свет является частным проявлением электромагнитных волн.
Дальнейшее развитие физики подтвердило это предположение. Стало ясно, что видимый свет — это только небольшой диапазон электромагнитных волн с длиной волны от 3,8•10-7 до 7,6•10-7 м или с частотами от 4,0•1014 до 8,0•1014 Гц (см. рис. 136).
Тем не менее представление о том, что в некоторых случаях свет ведёт себя аналогично потоку частиц, не потеряло своей актуальности.
К началу XX в. выяснилось, что электродинамика Максвелла не позволяет объяснить некоторые экспериментальные факты. Противоречия между теорией и экспериментальными данными удалось разрешить, предположив, что свет обладает корпускулярными свойствами. В 1900 г. немецкий физик Макс Планк выдвинул гипотезу, что атомы испускают электромагнитную энергию отдельными порциями — квантами. Энергия Е каждой порции прямо пропорциональна частоте v излучения:
Е = hn,
где h — коэффициент пропорциональности, получивший название постоянной Планка.
В 1905 г. немецкий физик Альберт Эйнштейн выдвинул идею, согласно которой электромагнитные волны с частотой v можно рассматривать как поток квантов излучения с энергией Е = hn.
В настоящее время квант электромагнитного излучения называют также фотоном. Фотон (от греч. phos, photos — свет) — это элементарная частица, являющаяся квантом электромагнитного излучения (в том числе света). Фотон не обладает ни массой, ни зарядом и всегда распространяется со скоростью света.
Таким образом, свет обладает как волновыми, так и корпускулярными свойствами.
С увеличением частоты электромагнитного излучения в большей степени проявляются его корпускулярные свойства, т. е. свойства, присущие потоку частиц, и в меньшей — волновые. Из всех диапазонов электромагнитных волн наиболее ярко выраженными корпускулярными свойствами обладает гамма-излучение (см. рис. 136). Подробнее о гамма-квантах вы узнаете из следующей главы.
1. Каковы были представления учёных о природе света в начале XIX в.?
2. Чем была вызвана необходимость выдвижения гипотезы о существовании
светоносного эфира?
3. Какое предположение о природе света было сделано Максвеллом? Какие общие
свойства света и электромагнитных волн явились основанием для такого
предположения?
4. Как называется частица электромагнитного излучения?
В курсе физики 8 класса вы познакомились с явлением преломления света. Теперь вы знаете, что свет представляет собой электромагнитные волны определенного диапазона частот. Опираясь на знания о природе света, вы сможете понять физическую причину преломления и объяснить многие другие связанные с ним световые явления.
Согласно закону преломления света (рис. 141):
лучи падающий, преломлённый и перпендикуляр, проведённый к границе раздела двух сред в точке падения луча, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных двух сред.
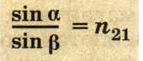 (1)
(1)
где n21 — относительный показатель преломления второй среды относительно первой.
Если луч переходит в какую-либо среду из вакуума, то
sin a / sin b = n (2)
где n — абсолютный показатель преломления (или просто показатель преломления) второй среды. В этом случае первой «средой» является вакуум, абсолютный показатель которого принят за единицу.
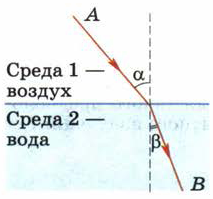
Рис. 141. Переходя из одной среды в другую, луч преломляется, т. е. меняет направление распространения
Закон преломления света был открыт опытным путём голландским учёным Виллебор-дом Снеллиусом в 1621 г. Закон был сформулирован в трактате по оптике, который нашли в бумагах учёного после его смерти.
После открытия Снеллиуса несколькими учёными была выдвинута гипотеза о том, что преломление света обусловлено изменением его скорости при переходе через границу двух сред. Справедливость этой гипотезы была подтверждена теоретическими доказательствами, выполненными независимо друг от друга французским математиком Пьером Ферма (в 1662 г.) и голландским физиком Христианом Гюйгенсом (в 1690 г.). Разными путями они пришли к одному и тому же результату, доказав, что
отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных двух сред, равная отношению скоростей света в этих средах:
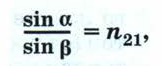
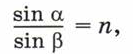 (3)
(3)
Из уравнения (3) следует, что если угол преломления b меньше угла падения a, то свет данной частоты во второй среде распространяется медленнее, чем в первой, т. е. V2<V1. Это означает, что вторая среда является оптически более плотной, чем первая.
Взаимосвязь величин, входящих в уравнение (3), послужила веским основанием для появления ещё одной формулировки определения относительного показателя преломления:
относительным показателем преломления второй среды относительно первой называется физическая величина, равная отношению скоростей света в этих средах:
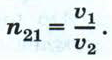 (4)
(4)
Пусть луч света переходит из вакуума в какую-либо среду. Заменив в уравнении (4) на скорость света в вакууме с, a v2 на скорость света в среде и, получим уравнение (5), являющееся определением абсолютного показателя преломления:
абсолютным показателем преломления среды называется физическая величина, равная отношению скорости света в вакууме к скорости света в данной среде:
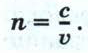 (5)
(5)
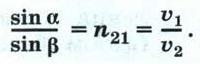
Значение абсолютного показателя преломления п любого вещества больше единицы (в этом убеждают данные, содержащиеся в таблицах физических справочников). Тогда, согласно уравнению (5), c/V > 1 и c > V, т. е. скорость света в любом веществе меньше скорости света в вакууме.
Не приводя строгих обоснований (они сложны и громоздки), отметим, что причиной уменьшения скорости света при его переходе из вакуума в вещество является взаимодействие световой волны с атомами и молекулами вещества. Чем больше оптическая плотность вещества, тем сильнее это взаимодействие, тем меньше скорость света и тем больше показатель преломления. Таким образом, скорость света в среде и абсолютный показатель преломления определяются свойствами этой среды.
По числовым значениям показателей преломления веществ можно сравнивать их оптические плотности. Например, показатели преломления различных сортов стекла лежат в пределах от 1,470 до 2,040, а показатель преломления воды равен 1,333. Значит, стекло — среда оптически более плотная, чем вода.
Обратимся к рисунку 142, с помощью которого можно пояснить, почему на границе двух сред с изменением скорости меняется и направление распространения световой волны.
Рис. 142. При переходе световых волн из воздуха в воду скорость света уменьшается, фронт волны, а вместе с ним и её скорость меняют направление
На рис. изображена световая волна, переходящая из воздуха в воду и падающая на границу раздела этих сред под углом a. В воздухе свет распространяется со скоростью v1 а в воде — с меньшей скоростью V2.
Первой до границы доходит точка А волны. За промежуток времени Δt точка В, перемещаясь в воздухе с прежней скоростью v1 достигнет точки В'. За то же время точка А, перемещаясь в воде с меньшей скоростью v2, пройдёт меньшее расстояние, достигнув только точки А'. При этом так называемый фронт волны А'В' в воде окажется повёрнутым на некоторый угол по отношению к фронту АВ волны в воздухе. А вектор скорости (который всегда перпендикулярен к фронту волны и совпадает с направлением её распространения) поворачивается, приближаясь к прямой ОО', перпендикулярной к границе раздела сред. При этом угол преломления р оказывается меньше угла падения a. Так происходит преломление света.
Из рисунка видно также, что при переходе в другую среду и повороте волнового фронта меняется и длина волны: при переходе в оптически более плотную среду уменьшается скорость, длина волны тоже уменьшается (l2 < l1 ). Это согласуется и с известной вам формулой l = v/n, из которой следует, что при неизменной частоте n (которая не зависит от плотности среды и поэтому не меняется при переходе луча из одной среды в другую) уменьшение скорости распространения волны сопровождается пропорциональным уменьшением длины волны.
1. Какое из двух веществ является оптически более плотным?
2. Как определяются показатели преломления через скорость света в средах?
3. Где свет распространяется с наибольшей скоростью?
4. Какова физическая причина уменьшения скорости света при его переходе из вакуума в среду или из среды с меньшей оптической плотностью в среду с большей?
5. Чем определяются (т. е. от чего зависят) абсолютный показатель преломления среды и скорость света в ней?
6*. Расскажите, что иллюстрирует рисунок 142.

1. Какие из трёх величин — длина волны, частота и скорость распространения волны — изменятся при переходе волны из вакуума в алмаз?
2. Используя рисунок 143, докажите, что относительный показатель преломления п21 для данных двух сред не зависит от угла падения луча света.
3. Какая из двух сред (рис. 144) обладает большей оптической плотностью? В какой из них луч света распространяется с большей скоростью? Ответ обоснуйте.
4*. Используя уравнения (4) и (5), докажите, что n21 = n2/n2, где n1, — абсолютный показатель преломления первой среды, а n2 — второй.
Указание: выразите из уравнения (5) скорость v света в среде через с и n ; по аналогии с полученной формулой запишите формулы для определения скоростей v1 и v2, входящих в уравнение (4); замените в уравнении (4) и v2 на соответствующие им буквенные выражения и упростите полученную формулу.
Вы уже знаете, что абсолютный показатель преломления среды определяется её свойствами.
Являются ли свойства среды единственным фактором, определяющим показатель преломления, или существуют какие-либо другие причины, от которых он зависит?
Для ответа на этот вопрос проделаем опыт, изображённый на рис. 145 (все изображённые на рис. предметы размещены на классной доске с металлической основой и удерживаются на ней благодаря имеющимся на них магнитам). Разместим около объектива осветителя О диафрагму Д с горизонтальной щелью (расположенной перпендикулярно плоскости чертежа) и синий светофильтр Ф (т. е. синее стекло). При этом на экране (роль которого выполняет укреплённая на доске и немного отогнутая бумажная полоска) на уровне световых лучей получится изображение щели синего цвета (на рис. 145, а его положение обозначено символом С1).
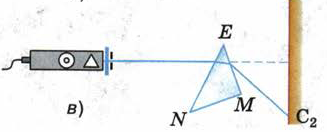
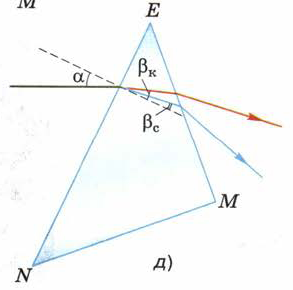
Рис. 145. Наблюдение дисперсии света при преломлении в призме световых лучей разной частоты
Заменим синий фильтр на красный — и на том же месте вместо синего изображения щели увидим красное К1.
Теперь на пути красного светового пучка поставим треугольную стеклянную призму NEM (рис. 145, б; объёмное изображение призмы — на рис. 145, г). Проходя через призму, луч отклоняется в сторону более широкой её части NM, в результате чего изображение щели смещается вниз в положение К2.
Проделаем тот же опыт, предварительно заменив красный светофильтр на синий (рис. 145, в). Мы обнаружим, что изображение щели, полученное в синих лучах, прошедших через призму, окажется в положении С2, т. е. сместится в том же направлении, что и красное, но на большее расстояние.
Проведённый опыт свидетельствует о том, что лучи синего цвета, имеющие большую частоту, чем красные, преломились сильнее красных. Это означает, что абсолютный показатель преломления стекла, из которого изготовлена призма, зависит не только от свойств стекла, но и от частоты (от цвета) проходящего через него света.
Из рисунка 145, д видно, что уже на грани NE призмы при одном и том же угле падения а синий луч преломился сильнее красного:
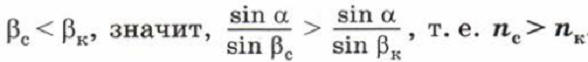
Соответственно для синих лучей больше и оптическая плотность стекла, но скорость их распространения в стекле меньше скорости красных, поскольку скорость обратно пропорциональна показателю преломления:
v = c / n
Зависимость показателя преломления вещества и скорости света в нём от частоты световой волны называется дисперсией света.
Слово «дисперсия» происходит от латинского dispersio и означает «рассеяние, развеивание».
Теперь, убрав с осветителя фильтр, пропустим через призму пучок белого света (рис. 146). Мы увидим, что этот пучок не только отклонился к более широкой части призмы, но и разложился в спектр1, в котором семь цветов — красный, оранжевый, жёлтый, зелёный, голубой, синий и фиолетовый (как в радуге) — плавно переходят друг в друга.
1 В данном случае под спектром понимается совокупность частот или длин волн, содержащихся в излучении какого-либо вещества. (В общем случае в физике спектр — это совокупность всех значений какой-либо физической величины, характеризующей систему или процесс.)
Рис. 146. Разложение пучка белого света в спектр
Рис. 147. Сложение спектральных цветов с помощью линзы
Это наводит на мысль, что белый свет является сложным, состоящим из световых волн разных цветов (и соответственно разных частот).
Синий и красный лучи, выделенные в предыдущем опыте из белого света с помощью фильтров, при прохождении через призму не разлагались в спектр. Это говорит о том, что цветные лучи являются простыми, или, как их ещё называют, монохроматическими (от греческих слов monos — один, единственный и chromatikos — цветной, окрашенный). Свет каждого цвета представлен волнами настолько узкого интервала частот, что обычно его характеризуют одной определённой частотой.
Чтобы удостовериться, что призма не окрашивает, а именно разлагает белый свет, поставим на пути вышедшего из призмы и разложившегося в спектр пучка собирающую линзу (рис. 147). Мы увидим, что после преломления в линзе разноцветные лучи, пересекаясь в точке А, «складываются», приобретая белый цвет.
Рис. 148. Опыт по сложению спектральных цветов
Рис. 149. Установка для получения сплошного спектра и объяснения того, почему окружающие нас тела,
освещённые солнечным светом, имеют разные цвета
Сложить спектральные цвета и получить белый цвет можно и на более простом опыте. Возьмём картонный диск с изображёнными на нём разноцветными секторами и укрепим его на валу центробежной машины (рис. 148). При быстром вращении диска создаётся впечатление, что он белый.
Зададимся вопросом, почему окружающие нас тела, освещённые одним и тем же солнечным светом, имеют разные цвета. В чём заключается физическая причина такого различия?
Чтобы выяснить это, проделаем опыт. С помощью установки, изображённой на рис. 149, получим на белом экране (или на укреплённом на доске листе белой бумаги) спектр, изображённый на рис. 150, а. Закроем правую часть спектра широкой бумажной полоской, например зелёного цвета. Мы увидим, что цвет полоски остаётся ярко-зелёным и не меняет оттенка только в той области, где на неё падают зелёные лучи. А при освещении лучами других цветов она либо меняет оттенок (в жёлтой части спектра), либо выглядит тёмной (рис. 150, б).
Значит, покрывающая полоску краска обладает способностью отражать только зелёный свет и поглощать свет всех остальных цветов.
Мы повторили с вами опыты, которые проделал И. Ньютон в 1666 г. Он пропускал через призму узкий пучок солнечного света, проходящего через маленькое отверстие в ставне.
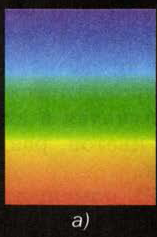

Рис. 150. Сплошной (непрерывный) спектр
В настоящее время для получения чётких и ярких спектров используют специальные оптические приборы.
На рис. 151 показано устройство и внешний вид одного из таких приборов — двухтрубного спектроскопа.
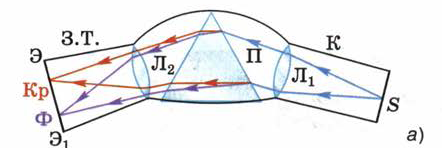
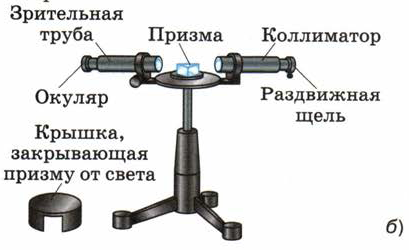
Рис. 151. Схема устройства и внешний вид двухтрубного спектроскопа
Рассмотрим принцип действия спектроскопа. В трубе К (рис. 151, а), называемой коллиматором, имеется узкая щель S. Через эту щель исследуемый свет входит в прибор и расширяющимся пучком падает на линзу Лг. Поскольку щель S расположена в фокальной плоскости этой линзы, то свет выходит из линзы параллельным пучком, а затем падает на призму П.
Так как волны разных цветов (т. е. разных частот) отклоняются призмой на разные углы, то из призмы выходят параллельные пучки разного направления (на рис. показаны крайние лучи только двух пучков — красного и фиолетового). Эти пучки, преломившись в линзе JI2, образуют в её фокальной плоскости ЭЭг изображения щели S. Причём изображения, соответствующие волнам разных частот, приходятся на разные места плоскости 33v
Если на щель падает белый свет, то все изображения щели сливаются в цветную полосу, в которой представлены все цвета.
Если же исследуемый свет представляет собой смесь нескольких монохроматических (простых) цветов, то спектр получится в виде узких линий соответствующих цветов, разделённых тёмными промежутками.
В спектрографе в плоскости ЭЭХ помещается фотопластинка, на которой получается фотография спектра. Фотография спектра называется спектрограммой.
Если же в плоскость ЭЭ1 поместить матовое стекло, то образующийся на нём спектр можно наблюдать глазом, увеличив изображение с помощью линзы. В этом случае прибор называется спектроскопом. Внешне спектрограф и спектроскоп выглядят одинаково (рис. 151, б).
На рис. 152 показан однотрубный спектроскоп (внешний вид — рис. а; устройство — рис. б и в). В школе его обычно используют при выполнении лабораторных работ по оптике. В том, как он действует, вы разберётесь самостоятельно при выполнении задания 3 из упражнения 45.

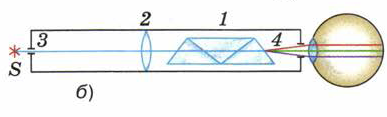
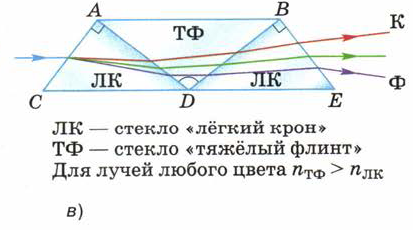
Рис. 152. Внешний вид и схема устройства однотрубного спектроскопа, применяемого при выполнении школьных лабораторных работ по оптике
Спектроскоп был сконструирован в 1815 г. немецким физиком Йозефом Фраунгофером. Этот прибор был необходим учёному для исследования явления дисперсии, которым он занимался в то время.
1. Что называется дисперсией света?
2. Расскажите об опыте по преломлению белого света в призме. (Ход опыта, результаты, вывод.)
3. Расскажите об опыте, изображённом на рис. 152.
4. В чём заключается физическая причина различия цветов окружающих нас тел?
5. Используя рисунок 151, расскажите об устройстве спектрографа.
6. Что такое спектрограмма?
7. Чем спектрограф отличается от спектроскопа?
1. На столе в тёмной комнате лежат два листа бумаги — белый и чёрный. В центре каждого листа наклеен оранжевый круг. Что вы увидите, осветив эти листы белым светом; оранжевым светом такого же оттенка, как и круг?
2. Напишите на белом листе бумаги первые буквы названий всех цветов спектра фломастерами соответствующих цветов: К — красным, О — оранжевым, Ж — жёлтым и т. д. Рассмотрите буквы через трёхсантиметровый слой ярко окрашенной прозрачной жидкости, налитой в тонкостенный стакан. Запишите результаты наблюдений и объясните их.
Указание: в качестве указанной жидкости можно использовать, например, малиновый или лимонный сироп, различные соки и т. п.
3. Рассмотрите рисунок 152, в и объясните, почему при входе в призму ADB лучи отклоняются в сторону более широкой её части (угол преломления меньше угла падения), а при входе в призму DBE — в сторону более узкой её части (угол преломления больше угла падения).
В опыте, изображённом на рис. 149, при пропускании солнечного света через призму получался спектр в виде сплошной полосы. В ней были представлены все цвета (т. е. волны всех частот от 4,0 • 1014 до 8,0 • 1014 Гц), плавно переходящие один в другой. Такой спектр называется сплошным или непрерывным (см. рис. 150, а).

Рис. 153. При внесении в пламя газовой горелки кусочка поваренной соли пламя окрасится в жёлтый цвет
Сплошной спектр характерен для твёрдых и жидких излучающих тел, имеющих температуру порядка нескольких тысяч градусов Цельсия. Сплошной спектр дают также светящиеся газы и пары, если они находятся под очень высоким давлением (т. е. если силы взаимодействия между их молекулами достаточно велики).
Например, сплошной спектр можно увидеть, если направить спектроскоп на свет от раскалённой нити электрической лампы ( tнити » 2800 °С), светящуюся поверхность расплавленного металла, пламя свечи. В этом случае свет излучается мельчайшими раскалёнными твёрдыми частицами (каждая из которых состоит из огромного числа взаимодействующих между собой атомов).
Иной вид имеет спектр, если в качестве источника света использовать светящиеся газы малой плотности. Такие газы обычно состоят из изолированных атомов, т. е. атомов, взаимодействие между которыми пренебрежимо мало. Свечения газа можно добиться, нагрев его до температуры порядка 2000 °С или более высокой.
Например, если внести в пламя спиртовки кусочек поваренной соли (рис. 153), то пламя окрасится в жёлтый цвет, а в спектре, наблюдаемом с помощью спектроскопа, будут видны две близко расположенные жёлтые линии, характерные для спектра паров натрия (рис. 154, а).
Это означает, что под действием высокой температуры молекулы NaCl распались на атомы натрия и хлора. Свечение атомов хлора возбудить гораздо труднее, чем атомов натрия, поэтому в данном опыте линии хлора не видны. Другие химические элементы дают другие наборы отдельных линий определённых длин волн (рис. 154, б и в).






Рис. 154. Спектры испускания: а — натрия; б — водорода; в — гелия.
Спектры поглощения: г — натрия; д — водорода; е —
гелия.
Такие спектры называются линейчатыми. Линейчатые спектры получают от газов и паров малой плотности, при которой свет излучается изолированными атомами.
Описанные выше спектры — сплошные и линейчатые — называются спектрами испускания.
Кроме спектров испускания существуют так называемые спектры, поглощения. Из всех спектров поглощения будем рассматривать только линейчатые.
Линейчатые спектры поглощения дают газы малой плотности, состоящие из изолированных атомов, когда сквозь них проходит свет от яркого и более горячего (по сравнению с температурой самих газов) источника, дающего непрерывный спектр.




Рис. 155. Идентификация по уникальным особенностям объекта
Линейчатый спектр поглощения можно получить, например, если пропустить свет от лампы накаливания через сосуд с парами натрия, температура которых ниже температуры нити лампы накаливания. В этом случае в сплошном спектре света от лампы появится узкая чёрная линия как раз в том месте, где располагается жёлтая линия в спектре испускания натрия (сравните рисунки 154, а и г). Это и будет линейчатый спектр поглощения натрия. Другими словами, линии поглощения атомов натрия точно соответствуют его линиям испускания.
Совпадение частот линий испускания и поглощения можно наблюдать и в спектрах других элементов, например водорода и гелия (рис. 154, б, д и в, е).
Общий для всех химических элементов закон, согласно которому -
атомы данного элемента поглощают световые волны тех же самых частот, на которых они излучают,
- был открыт в середине XIX в. немецким физиком Густавом Кирхгофом.

ГУСТАВ КИРХГОФ
(1824—1887)
Немецкий физик. Разработал метод спектрального анализа и открыл элементы - цезий и рубидий,
установил закон теплового излучения
.
Спектр атомов каждого химического элемента уникален. Как не бывает двух людей с одинаковым дактилоскопическим узором1 или двух китов с одинаковой окраской хвостового плавника, так и не существует двух химических элементов, атомы которых излучали бы одинаковый набор спектральных линий (рис. 155).
Благодаря этому стало возможным появление метода спектрального анализа, разработанного в 1859 г. Кирхгофом и его соотечественником, немецким химиком Р. Бунзеном.1 Расположение рельефных линий кожи на внутренних (ладонных) поверхностях ногтевых фаланг пальцев рук.
Спектральным анализом называется метод определения химического состава вещества по его линейчатому спектру.
Для проведения спектрального анализа исследуемое вещество приводят в состояние атомарного газа (атомизируют) и одновременно с этим возбуждают атомы, т. е. сообщают им дополнительную энергию.
Для атомизации и возбуждения используют высокотемпературные источники света: пламя или электрические разряды. В них помещают образец исследуемого вещества в виде порошка или аэрозоля раствора (т. е. мельчайших капелек раствора, распылённого в воздухе). Затем с помощью спектрографа получают фотографию спектров атомов элементов, входящих в состав данного вещества.
В настоящее время существуют таблицы спектров всех химических элементов. Отыскав в таблице точно такие же спектры, какие были получены при анализе исследуемого образца, узнают, какие химические элементы входят в его состав. Путём сравнения интенсивности линий определяют количество каждого элемента в образце.
Спектральный анализ отличается от химического анализа своей простотой, высокой чувствительностью (например, с его помощью можно обнаружить наличие химического элемента, масса которого в данном образце не превышает 10-10 г), а также возможностью определять химический состав отдалённых тел, например звёзд.
Он используется для контроля состава вещества в металлургии, машиностроении и атомной индустрии. Этот метод применяется также в геологии, археологии, криминалистике и многих других сферах деятельности. В астрономии методом спектрального анализа определяют химический состав атмосфер планет и звёзд, температуру звёзд и магнитную индукцию их полей. По смещению спектральных линий в спектрах галактик была определена их скорость, и на основании этого сделан вывод о расширении нашей Вселенной.
1, Как выглядит сплошной спектр? Какие тела дают сплошной спектр? Приведите
примеры.
2. Как выглядят линейчатые спектры? От каких источников света получаются
линейчатые спектры?
3. Каким образом можно получить линейчатый спектр испускания натрия?
4. Опишите механизм получения линейчатых спектров поглощения.
5. В чём заключается суть закона Кирхгофа, касающегося линейчатых спектров испускания и поглощения?
6*. Что такое спектральный анализ и как он проводится?
7*. Расскажите о применении спектрального анализа.
В процессе изучения и применения линейчатых спектров возникли различные вопросы. Как, например, объяснить, почему атомы каждого химического элемента имеют свой строго индивидуальный набор спектральных линий? Почему совпадают линии излучения и поглощения в спектре данного элемента? Чем обусловлены различия в спектрах атомов разных элементов?
Ответы на эти и многие другие вопросы удалось найти только в начале XX в. благодаря возникновению новой физической теории — квантовой механики. Одним из основоположников этой теории был датский физик Нильс Бор.

НИЛЬС
БОР
(1885—1962)
Датский физик-теоретик, общественный деятель, один из создателей современной физики. Создал теорию водородоподобного атома, основанную на двух постулатах
Бор пришёл к заключению, что свет излучается атомами вещества. В связи с этим в 1913 г. он сформулировал два постулата.
Постулат 1. Атом может находиться только в особых, стационарных состояниях. Каждому состоянию соответствует определённое значение энергии — энергетический уровень. Находясь в стационарном состоянии, атом не излучает и не поглощает.
Стационарным состояниям соответствуют стационарные орбиты, по которым движутся электроны. Номера стационарных орбит и энергетических уровней (начиная с первого) в общем случае обозначаются латинскими буквами: n, k и т. д. Радиусы орбит, как и энергии стационарных состояний, могут принимать не любые, а определённые дискретные значения. Первая орбита расположена ближе всех к ядру.
Постулат 2. Излучение света происходит при переходе атома из стационарного состояния с большей энергией Ек в стационарное состояние с меньшей энергией Еn.
Согласно закону сохранения энергии, энергия излучённого фотона равна разности энергий стационарных состояний:
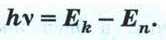
Из этого уравнения следует, что атом может излучать свет только с частотами:
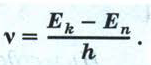
Атом может также поглощать фотоны. При поглощении фотона атом переходит из стационарного состояния с меньшей энергией в стационарное состояние с большей энергией.
Состояние атома, в котором все электроны находятся на стационарных орбитах с наименьшей возможной энергией, называется основным. Все другие состояния атома называются возбуждёнными.
У атомов каждого химического элемента имеется свой характерный набор энергетических уровней. Поэтому переходу с более высокого энергетического уровня на более низкий будут соответствовать характерные линии в спектре испускания, отличные от линий в спектре другого элемента.
Совпадение линий излучения и поглощения в спектрах атомов данного химического элемента объясняется тем, что частоты волн, соответствующих этим линиям в спектре, определяются одними и теми же энергетическими уровнями. Поэтому атомы могут поглощать свет только тех частот, которые они способны излучать.
1. Сформулируйте постулаты Бора.
2. Запишите уравнения для определения энергии и частоты излучённого фотона.
3. Какое состояние атома называют основным; возбуждённым?
4. Как объясняется совпадение линий в спектрах испускания и поглощения данного химического элемента?
В вашем распоряжении имеются две стальные спицы. Придумайте эксперименты, с помощью которых можно было бы определить: а) намагничена ли одна из спиц, и если да, то какая; б) намагничены ли обе спицы.
Примечание: в эксперименте могут быть использованы только указанные предметы.
Ниже даны, физические понятия, явления, правило, закон, постулаты и их определения и формулировки. Последовательность изложения определений не соответствует последовательности понятий.
Перенесите в тетрадь названия понятий и законов и впишите в квадратные скобки порядковый номер определения (формулировки), соответствующего данному понятию, явлению, постулату, правилу, закону.
■ Переменный ток [ ];
■ электромагнитная волна [ ];
■ радиосвязь [ ];
■ дисперсия света [ ];
■ явление электромагнитной индукции [ ];
■ правило Ленца [ ];
■ явление самоиндукции [ ];
■ закон преломления света [ ];
■ квантовые постулаты Бора [ ];
■ типы оптических спектров [ ].
1. Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует изменению магнитного потока, которое вызвало этот ток.
2. Отношение синуса угла падения к синусу угла преломления есть величина
постоянная для данных двух сред, равная отношению скоростей
света в этих средах: 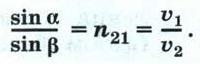
3. Возникновение индукционного тока в катушке при изменении силы тока в ней.
4. Атом может находиться только в особых, стационарных состояниях. Каждому состоянию соответствует определённое значение энергии — энергетический уровень. Находясь в стационарном состоянии, атом не излучает и не поглощает.
Излучение света происходит при переходе атома из стационарного состояния с большей энергией Ек в стационарное состояние с меньшей энергией Еп.
5. Электрический ток, периодически меняющийся по модулю и направлению.
6. Система порождающих друг друга и распространяющихся в пространстве переменных электрического и магнитного полей.
7. При всяком изменении магнитного потока, пронизывающего площадь, ограниченную замкнутым проводником, в этом проводнике возникает электрический ток, существующий в течение всего процесса изменения магнитного потока.
8. Передача и приём информации посредством электромагнитных волн.
9. Зависимость показателя преломления вещества и скорости света в нём от частоты световой волны.
10. Сплошной (непрерывный) характерен для жидких и твёрдых излучающих тел с температурой порядка нескольких тысяч градусов и для светящихся газов и паров, находящихся под очень большим давлением; линейчатый характерен для светящихся газов малой плотности при температуре порядка 2000 °С.
1. В данной системе отсчёта магнитное поле создаётся движущимися в ней:
A. фотонами
Б. электронами
B. атомами
Г. нейтронами
2. Магнитное поле обнаруживается по его действию на
A. покоящиеся в нём протоны Б. покоящиеся в нём нейтроны
B. покоящиеся в нём ионы
Г. проводник с протекающим по нему электрическим током
3. Магнитное поле характеризуется векторной физической величиной, которая обозначается символом В и называется
A. магнитной индуктивностью
Б. магнитной индукцией
B. электромагнитной индукцией
Г. самоиндукцией
4. Закону преломления света соответствует формула: