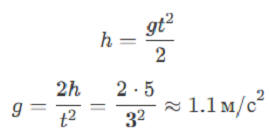
Смоделировать проблемные ситуации на уроке физики.
Отчет: подбор видео роликов или фильмов и постановка проблемных вопросов в результате решения которых ученики учатся самостоятельно мыслить и самостоятельно получать знания, анализировать и делать выводы.
Фрагмент из мультика про Винни-Пуха.
Падение Винни Пуха с дерева.
На уроке физики дать задание ученикам оценить параметры "физического мира" в
котором живут "Винни Пух и все-все-все":
1) Оценить ускорение свободного падения Пуха;
2) попробовать оценить сопротивление среды - то есть воздуха при падениии Пуха;
3) По объему шарика оценить массу Пуха и плотность атмосферы.
Первая итерация.
В мультфильме (1969 года) падение Винни-Пуха с дерева происходит очень медленно – несколько секунд, хотя высота дерева кажется значительной.
Если Пух падает с высоты h = 5 м и время падения t ≈ 3 с, то ускорение свободного падения можно оценить по формуле:
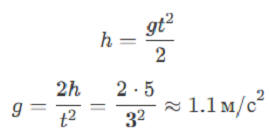
Ускорение свободного падения в мире Винни-Пуха примерно в 9 раз меньше, чем на Земле (g ≈ 1.1 м/с² против 9.8 м/с²).
Если падение медленное, значит, сила сопротивления воздуха компенсирует силу тяжести. Условие равномерного падения (без ускорения, предполагаем квадратичную зависимость силы сопротивления от скорости):
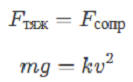
Оценка массы Пуха:
Допустим, Винни-Пух – это шар диаметром D ≈ 1 м (по
мультфильму).
Если он сделан из мёда и пуха, его плотность может быть близка к плотности воды
(ρ ≈ 1000 кг/м³).
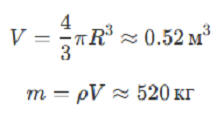
Но это слишком много! Вероятно, плотность Пуха гораздо меньше – допустим, как у пенопласта, ρ ≈ 50 кг/м³, тогда m ≈ 26 кг.
Расчёт скорости падения:
Если Пух падает 3 секунды с высоты 5 м, средняя скорость:
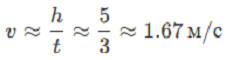
Коэффициент сопротивления (k):
.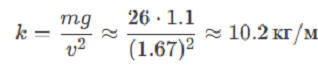
Для сравнения: на Земле при g = 9.8 м/с² и той же скорости k было бы около 90 кг/м.
Вывод:
Сопротивление воздуха в мире Винни-Пуха намного больше, чем на
Земле (либо плотность атмосферы выше, либо Пух обладает необычной
аэродинамикой).
Масса Пуха: Если принять более реалистичную плотность (ρ ≈ 50 кг/м³), то:Это многовато для плюшевого мишки, но в мультфильме он кажется тяжеловатым.
Плотность атмосферы: Сила сопротивления зависит от плотности воздуха (ρₐ), площади поперечного сечения (S) и коэффициента лобового сопротивления (Cₓ ≈ 0.5 для шара):
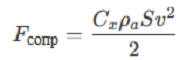 ,
,
![]() .
.
Подставляем:
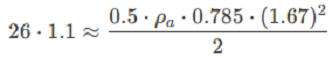 ,
,
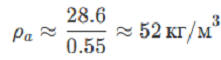
Плотность воздуха в мире Винни-Пуха в 40 раз выше, чем на Земле (на Земле ρₐ ≈ 1.225 кг/м³)!
Ускорение свободного падения (g) ≈ 1.1 м/с² (в 9 раз меньше земного).
Плотность атмосферы ≈ 52 кг/м³ (в 40 раз выше земной).
Масса Винни-Пуха ≈ 26 кг (если его плотность как у пенопласта).
Выводы: Либо мир Винни-Пуха находится на очень маленькой планете (с низкой g), но с невероятно плотной атмосферой, либо в этом мире другая физика (например, большая вязкость воздуха или малая гравитация), либо наши начальные положения не верны.
Вторая итерация.










Кадр: Винни-Пух влазит на последний сучек , отделяющий его от улья. Сучок ломается.
Действие: Пух с удивлением смотрит на обломок, начинает медленно крениться вбок и падает.
Фраза: «О-о-о, кажется, я падаю… ?»
Кадр: Пух плавно отделяется от ветки, начинает опускаться вниз кубарем.
Действие: Лапы раскинуты в стороны, шерсть дыбом. Скорость ~0.5 м/с.
Кадр: Пух медленно переворачивается в воздухе (на 180° за 2 секунды).
Действие: Вращение динамикой как у падающего листа.
Кадр: Пух теперь летит вниз то головой то лапами.
Действие: Скорость почти не увеличивается (~1 м/с), сопротивление воздуха огромное.
Кадр: Земля уже близко, но Пух не ускоряется. В кадре мелькают ветви дерева.
Действие: Пух пытается затормозить, размахивая лапами, но безрезультатно.
Кадр: Пух аккуратно шлепается в куст колючек.
Действие: Садится на задние лапы, передние лапы - вверх.
Ускорение свободного падения: (в 8 раз меньше земного). Падение похоже на движение в глицерине.
Плотность атмосферы: (в 4 раза выше земной).
Вязкость воздуха: (в 400 раз выше, чем на Земле).
Аниматоры намеренно игнорировали земную физику для создания комичного эффекта.
| Параметр | Мультфильм (1969) | Реальный мир (Земля) |
|---|---|---|
| Время падения с 5 м | 5 сек | 1 сек |
| Скорость приземления | ~1 м/с | ~10 м/с |
| Поведение тела | Плавное падение | Быстрый набор скорости |
Ви